Chat GPT / Stable Diffusion / 自動運転技術を筆頭に,今や AI といえば Deep Learning の時代といっても過言ではないでしょう(もちろん,スパースモデリングなども今後ブームとなる可能性もあります).
そして,その基礎となるのがこのニューラルネットワークです.
当該記事では,脳の神経細胞の数理モデルであるパーセプトロンから始まり,多層パーセプトロン,ニューラルネットワークへと紹介していきます.
当該記事のコードは github 上にも置いています.
パーセプトロン
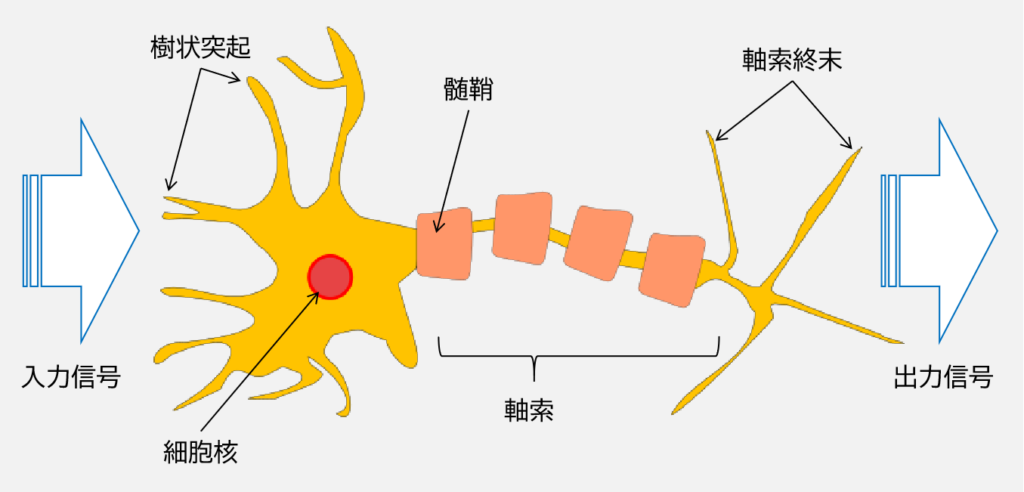
上図はニューロンの模式図です.
ニューロン (neuron) は神経細胞で,電気的/化学的な入力信号を処理/伝送する役割があります.
ヒトの脳全体には約1000億個ものニューロンがあると言われています (https://www.scj.go.jp/omoshiro/kioku2/index.html).
1943 年に Waren McCulloch と Walter Pitts によって,McCulloch-Pitts ニューロン(MCP ニューロン,または形式ニューロン (formal neuron) と呼ばれる)というニューロンを簡略化したモデルを提唱されました.
MCP ニューロンは,「複数の信号が樹状突起に届いてニューロンに取り込まれ,蓄積された信号が特定の閾値を超えた場合は出力信号が生成され,軸索によって伝達される」という働きを「二値出力を行う単純な論理ゲート」とモデル化したものです.
1957 年,Frank Rosenblatt はこの MCP ニューロンに対し,「最適な重み係数を自動的に学習した後,入力信号をかけ合わせ,ニューロンが発火する(信号の総和が閾値を超えて出力する)かどうかを判断する」というアルゴリズムを提案しました.
この人工的なニューロンはパーセプトロン (perceptron) と呼ばれます.
パーセプトロンは,現代のニューラルネットワークの起源となっています.
パーセプトロンの働きについて,次のような2入力1出力のパーセプトロンについて考えてみます.
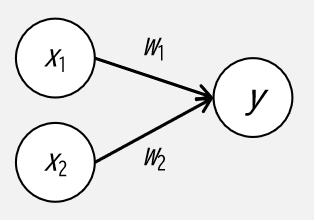
上図において,\(x_1, x_2\) は入力信号,\(y\) は出力信号,\(w_1, w_2\) は入力信号に対する重み(weight)を表します.
パーセプトロンの働きとしては,0 もしくは 1 を出力する二値分類タスクを行うものとして,数式では次で考えることができます.
$$
y =
\begin{cases}
0 & (w_1 x_1 + w_2 x_2 \le \theta) \\
1 & (w_1 x_1 + w_2 x_2 \gt \theta)
\end{cases}
$$
ここで \(\theta\) はニューロンが発火するかどうかを決める閾値を表し,ニューロンの発火のしやすさをコントロールする役割を持ちます.
例えば,\(y = 1\) となる式において以下のように変形できます.
$$
w_1 x_1 + w_2 x_2 \gt \theta \\
\iff x_2 \gt \ – \frac{w_1 x_1}{x_2} + \frac{\theta}{w_2} = f(x_1)
$$
上式は一次式の上側を表していますが,グラフ化するとこのようなイメージです.
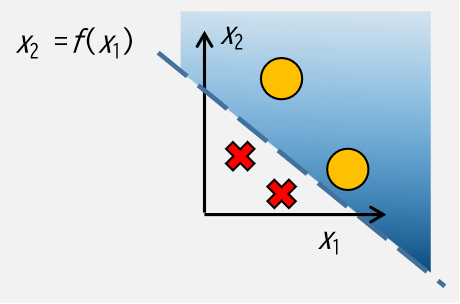
破線は決定境界の \(x_2 = f(x_1)\),青色に塗られた領域は \(x_2 > f(x_1)\),○と✕はある特定の2つのクラス(\(y\))を表します.
出力の式としては,一般的には閾値 \(\theta\) をバイアス \(b = – \theta\) とし,かつ,重みと入力はそれぞれベクトルとして,次式のように 0 に対する大小関係で書き表されます.
$$
y =
\begin{cases}
0 & (b + \boldsymbol{w}^T \boldsymbol{x} \le 0) \\
1 & (b + \boldsymbol{w}^T \boldsymbol{x} \gt 0)
\end{cases}
$$
上図では○と✕を分けることができていますが,これを実現するためには,この関数の重みとバイアスのパラメータを適切に設定しなければなりません.
この段階では,パラメータは学習データとなる○と✕の座標及びクラス値を元に人間が考えて決定する必要があります.
実際に次の論理回路を出力するようにパーセプトロンのパラメータを設計してみましょう.
まずは色々使うライブラリのインポートとプロットの関数について準備していきます.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
sns.set()def plot_gate(x1: np.ndarray, x2: np.ndarray, y: np.ndarray, title: str = None):
# プロットする関数
fig = plt.figure(figsize=(4, 4), facecolor="white")
ax = plt.axes(aspect="equal")
ax.scatter(x1, x2, c=y, cmap="coolwarm_r", s=300)
if title:
ax.set_title(title)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
fig.tight_layout()
plt.show()AND ゲート:
| x_1 | x_2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
# AND ゲート定義
x1 = np.array([0, 0, 1, 1], dtype=np.float32)
x2 = np.array([0, 1, 0, 1], dtype=np.float32)
y = np.array([0, 0, 0, 1], dtype=np.float32)
plot_gate(x1=x1, x2=x2, y=y, title="AND")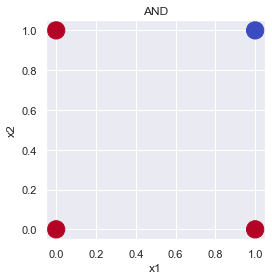
例えば,\((w_1, w_2, b) = (0.5, 0.5, -0.7)\) で,見た感じ直線一本(一次式)で分けられそうです.
AND ゲートを関数化し,出力を確かめてみましょう.
def and_gate(x1: float, x2: float) -> int:
# ベクトル化
x = np.array([x1, x2])
# パラメータ定義
w = np.array([0.5, 0.5])
b = - 0.7
# 入力ベクトルと重みの内積,バイアスを比較
if b + w.dot(x) > 0:
return 1
else:
return 0for i in range(4):
one_or_zero = and_gate(x1=x1[i], x2=x2[i])
print(f"x1 = {x1[i]}, x2 = {x2[i]} -> y = {one_or_zero}")
# x1 = 0.0, x2 = 0.0 -> y = 0
# x1 = 0.0, x2 = 1.0 -> y = 0
# x1 = 1.0, x2 = 0.0 -> y = 0
# x1 = 1.0, x2 = 1.0 -> y = 1AND ゲートの論理値表と全く同じ出力が得られましたね.
他の論理回路も順に考えていきましょう.
NAND ゲート:
| x_1 | x_2 | y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
# NAND ゲート定義
x1 = np.array([0, 0, 1, 1], dtype=np.float32)
x2 = np.array([0, 1, 0, 1], dtype=np.float32)
y = np.array([1, 1, 1, 0], dtype=np.float32)
plot_gate(x1=x1, x2=x2, y=y, title="NAND")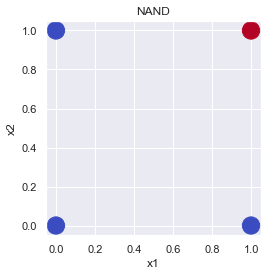
def nand_gate(x1: float, x2: float) -> int:
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
if b + w.dot(x) > 0:
return 1
else:
return 0for i in range(4):
one_or_zero = nand_gate(x1=x1[i], x2=x2[i])
print(f"x1 = {x1[i]}, x2 = {x2[i]} -> y = {one_or_zero}")
# x1 = 0.0, x2 = 0.0 -> y = 1
# x1 = 0.0, x2 = 1.0 -> y = 1
# x1 = 1.0, x2 = 0.0 -> y = 1
# x1 = 1.0, x2 = 1.0 -> y = 0OR ゲート:
| x_1 | x_2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
# OR ゲート定義
x1 = np.array([0, 0, 1, 1], dtype=np.float32)
x2 = np.array([0, 1, 0, 1], dtype=np.float32)
y = np.array([0, 1, 1, 1], dtype=np.float32)
plot_gate(x1=x1, x2=x2, y=y, title="NAND")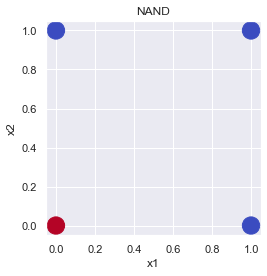
def or_gate(x1: float, x2: float) -> int:
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = - 0.2
if b + w.dot(x) > 0:
return 1
else:
return 0for i in range(4):
one_or_zero = or_gate(x1=x1[i], x2=x2[i])
print(f"x1 = {x1[i]}, x2 = {x2[i]} -> y =: {one_or_zero}")
# x1 = 0.0, x2 = 0.0 -> y =: 0
# x1 = 0.0, x2 = 1.0 -> y =: 1
# x1 = 1.0, x2 = 0.0 -> y =: 1
# x1 = 1.0, x2 = 1.0 -> y =: 1ここまでは問題なく適切なパラメータを定義できたことでしょう.
では,こちらはどうでしょうか?
XOR ゲート:
| x_1 | x_2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
# XOR ゲート定義
x1 = np.array([0, 0, 1, 1], dtype=np.float32)
x2 = np.array([0, 1, 0, 1], dtype=np.float32)
y = np.array([0, 1, 1, 0], dtype=np.float32)
plot_gate(x1=x1, x2=x2, y=y, title="XOR")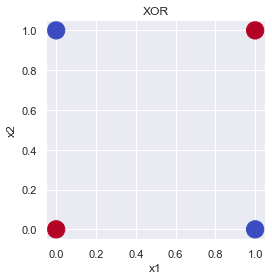
どう頑張っても直線(1次式)で赤と青を分けることはできませんね.
(SVM の記事 (https://slash-z.com/svm-support-vector-machine/) では線形分離不可能と紹介いたしました.)
そこで登場するのが,このパーセプトロンを多層化するという考えです.
多層パーセプトロン
多層パーセプトロン (multi-layered perceptron; MLP) とは層を複数重ねたパーセプトロンであり,前の章で扱ったのは,言うなれば単層(単純)パーセプトロンということになります.
イメージとしては下図です.
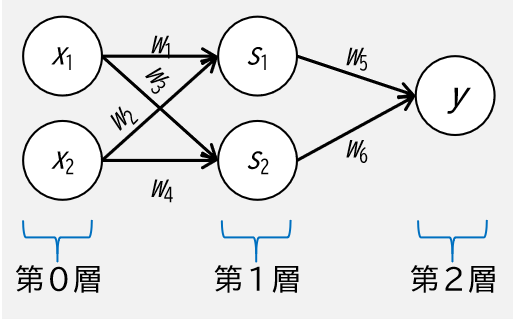
単純パーセプトロンと比較すると第1層が増え,第0層から第1層への重みも増えました.
しかし考え方は同じで,出力側の第2層から順番に定式化していくと以下のようになります.
$$
y =
\begin{cases}
0 & (w_5 s_1 + w_6 s_2 \le \theta_2) \\
1 & (w_5 s_1 + w_6 s_2 \gt \theta_2)
\end{cases}
$$
$$
s_1 =
\begin{cases}
0 & (w_1 x_1 + w_2 x_2 \le \theta_1) \\
1 & (w_1 x_1 + w_2 x_2 \gt \theta_1)
\end{cases}
$$
$$
s_2 =
\begin{cases}
0 & (w_3 x_1 + w_4 x_2 \le \theta_1) \\
1 & (w_3 x_1 + w_4 x_2 \gt \theta_1)
\end{cases}
$$
それでは,上図のような多層パーセプトロンで XOR ゲートを考えてみましょう.
\(x_1, \ x_2, \ y\) の値はそれぞれ固定なので,\(s_1, \ s_2\) の値がどうなっていれば良いかについて考えると,
XOR ゲート(多層パーセプトロン ver.):
| x_1 | x_2 | s_1 | s_2 | y |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
という具合に \(s_1, \ s_2\) を設定すれば,\(y\) は第1層から AND ゲートで出力できそうです.
一方,この \(s_1, \ s_2\) はどちらも \(x_1, \ x_2\) で表現できますが,\(s_1\) は OR ゲート, \(s_2\) は NAND ゲートで表現できます.
つまり,関数の処理自体も多層化するだけで新たな表現が可能になるということです.
実際に今まで設計したゲートで XOR ゲートをコード実装すると次のようになります.
def xor_gate(x1: float, x2: float) -> int:
s1 = or_gate(x1=x1, x2=x2)
s2 = nand_gate(x1=x1, x2=x2)
y = and_gate(x1=s1, x2=s2)
return yfor i in range(4):
one_or_zero = xor_gate(x1=x1[i], x2=x2[i])
print(f"x1 = {x1[i]}, x2 = {x2[i]} -> y =: {one_or_zero}")
# x1 = 0.0, x2 = 0.0 -> y =: 0
# x1 = 0.0, x2 = 1.0 -> y =: 1
# x1 = 1.0, x2 = 0.0 -> y =: 1
# x1 = 1.0, x2 = 1.0 -> y =: 0コードを見ても明らかですが,ここでは重みの設計は一切行っておらず,既存のゲートを再利用するだけで XOR ゲートが実現できました.
このようにパーセプトロンを積層するだけで,線形的な表現だけでなく,非線形的な複雑な表現力を持つことができます.
ニューラルネットワーク
パーセプトロンを多層化することで多様な表現力を持つことが分かりました.
しかし,得られる入力から欲しい出力を得るためにパーセプトロンを構築するには,自分で適切な重みを設定する必要がありました.
対してニューラルネットワーク (Neural Network; NN,人工ニューラルネットワークとも呼ばれる) では,パーセプトロンではできなかった適切なパラメータをデータから自動で学習することができます.
これがデータ駆動 (data driven) と言われる所以です.
ところで名称の定義ですが,書籍や記事によっては,「多層パーセプトロン」=「ニューラルネットワーク」としているものもありますが,当該記事では,上記の通り,「パーセプトロンでは学習ができないモデル」といった初期構想を尊重してこれを定義し,データから重みが学習できない/できるで両者の呼び方をあえて分けています.
(何でも,「最初に考えた人ややった人って偉いよなぁ」という個人的な思いがあります.)
しかしながら,一般的には,”「単純パーセプトロン」は単層のネットワークで活性化関数にステップ関数を用いたもの”,”「多層パーセプトロン」は「ニューラルネットワーク」と同義であり多層のネットワークでシグモイド関数などのなめらかな活性化関数を使用するもの”,とされているようです(参考書籍: 「ゼロから作る Deep Learning」).
ニューラルネットワークのイメージとしては具体的には下図のようなもので,ここでは例として4つの層からなる全結合層(層と層のニューロンが全て連結されている層)のみのニューラルネットワークを図示しています.
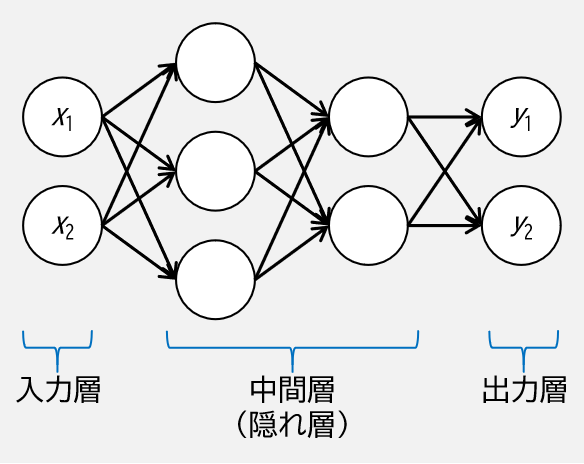
中間層は入力層や出力層と異なり,通常目に見えないブラックボックス化された層であり,隠れ層 (hidden layer) とも呼ばれます.
この図を見ると,多層パーセプトロンと何ら変わりないように見えます.
では,どうやってデータから自動で学習できるようになったかというと,ハードウェアの進化の話はおいといて,
- 活性化関数
- 損失関数
- 確率的勾配降下法
- 誤差逆伝播
を追加したことによります.
学習の流れとしては以下です.
- 学習データからランダムに一部のデータ(ミニバッチ)を取得
- ミニバッチのニューラルネットワーク出力と正解データの乖離を損失関数によって算出
- 重みの勾配(損失を減らす方向)を求める
- 求めた勾配方向に重みを微小量だけ更新していく
- 1~4を繰り返すことで重みが最適化していく
これらについて順に説明していきます.
活性化関数
パーセプトロンでは,層の出力値ベクトルと重みベクトルの内積が指定した閾値 \(\theta\) よりも大きい場合に発火(1を出力)し,その以外では発火しない(0を出力する)というものでした.
バイアス \(b = – \theta\) とした単純パーセプトロンの入力と出力の関係式は以下でした.
$$
y =
\begin{cases}
0 & (b + \boldsymbol{w}^T \boldsymbol{x} \le 0) \\
1 & (b + \boldsymbol{w}^T \boldsymbol{x} \gt 0)
\end{cases}
$$
上記の場合分けによる式について,発火する/しないを決定する関数を \(h\),0に対する大小が評価される関数(つまり条件式の右辺)を \(a\) とすると,上式は次式で書き表せます.
$$
y = h(a) \\
a = b + \boldsymbol{w}^T \boldsymbol{x} \\
h(a) =
\begin{cases}
0 & (a \le 0) \\
1 & (a \gt 0)
\end{cases}
$$
この \(h\) を活性化関数 (activation function) と言います.
多層パーセプトロンでは,閾値に対する大小関係によって0か1が出力されるステップ関数 (step function) を用いていました.
しかし,ステップ関数では0か1といった論理値しか出力できません.
そこでニューラルネットワークでは,浮動小数点数が出力できるような活性化関数を採用することで,発火する/しないだけでなく,伝送する情報量を調整することができます.
例えば出力層に限って言うと,ステップ関数では各出力において0か1しか表現できませんが,浮動小数点数を扱えるような活性化関数を用いることによって,どのくらいの確信度 (confidence score) になっているかをそれぞれの出力で表現することができます.
以下に,代表的な活性化関数を列挙していきます.
シグモイド関数
シグモイド関数 (sigmoid function) は次式で定義されます.
$$
h(x) = \frac{1}{1 + \exp{(-x)}}
$$
ReLU 関数
ReLU 関数 (Rectified Linear Unit,読み方は「レル」) は次式で定義されます.
$$
h(x) =
\begin{cases}
x & (x \gt 0) \\
0 & (x \le 0)
\end{cases}
$$
Softmax 関数
Softmax 関数は次式で定義されます.
$$
y_k = \frac{\exp{(x_k)}}{\sum_{i=1}^{n} \exp{(x_i)}}
$$
ここで,\(y_k\) は \(k\) 番目の出力,\(n\) は出力の数を表します.
Softmax 関数だけ数式の見た目が違いますが,これは各出力 \(y_k\) に対し各入力 \(x_k\) が作用するためで,一般的には多クラス分類に用いられます.
実際2クラス分類だと \(n = 2\) なので,
$$
y_1 = \frac{\exp{(x_1)}}{\exp{(x_1) + \exp{(x_2)}}} = \frac{1}{1 + \exp{(x_2 – x_1)}} \\
y_2 = \frac{\exp{(x_2)}}{\exp{(x_1) + \exp{(x_2)}}} = \frac{1}{1 + \exp{(x_1 – x_2)}}
$$
なので,Softmax 関数はシグモイド関数を多クラス分類に拡張したものといえます.
活性化関数の比較
パーセプトロンにて用いていたステップ関数も含めて活性化関数を図示してみましょう.
# x 定義
dx = 0.05
x = np.arange(-5, 5 + dx, dx).astype(dtype=np.float32)
# 各関数定義
step_fn = (x > 0).astype(dtype=np.uint8)
sigmoid_fn = 1 / (1 + np.exp(-x))
relu_fn = np.maximum(0, x)
# プロット
plt.figure(figsize=(5, 4), facecolor="white")
plt.plot(x, step_fn, label="Step fn.", color="gray", linestyle="--")
plt.plot(x, sigmoid_fn, label="Sigmoid fn.")
plt.plot(x, relu_fn, label="ReLU fn.")
plt.ylim(-0.1, 1.1)
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="upper left")
plt.tight_layout()
plt.show()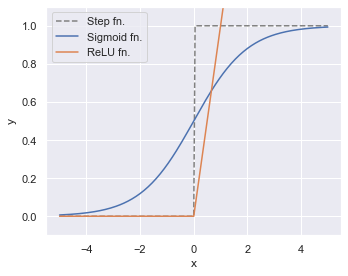
このように,シグモイド関数/ReLU 関数では浮動小数点数の表現が可能です.
シグモイド関数は任意の \(x\) に対し0から1を返すようになっていて,二値分類の出力層に用いられます.
ReLU 関数は0以下だと0,0より大きいとその大きさに比例した \(x\) を返すようになっていて,単純な計算であり計算コストが低いことから隠れ層に良く用いられます.
損失関数
ニューラルネットワークを学習させるためには,ニューラルネットワークの出力である推論結果に対してどの程度良い/悪いを判断して重みを最適な値へ更新していく必要がありますが,このときの判断基準となるものが損失関数 (loss function) です.
損失関数はニューラルネットワークの性能がどのくらい悪いかを判断する指標で,ニューラルネットワーク出力と正解となる教師データの乖離を何らかの形で定量的に評価する関数です.
これを最小化するように重みを更新していく(学習する)ことにより,性能が良くなっていきます.
代表的な損失関数について以下に列挙していきます.
二乗平均誤差
二乗平均誤差 (Mean Squared Error; MSE) は次式で定義されます.
$$
E = \frac{1}{2} \sum_{k=1}^{n} {(y_k – t_k)^2}
$$
ここで,\(y\) はニューラルネットワークの出力,\(t\) は教師データ,\(n\) はデータの次元数を表します.
「平均」とついていながら \(n\) で割っていないのは,各出力と比較して誤差の程度の大きさや大小関係さえ見れれば良いので,係数は何でも良いことから省略されています.
また,2で除算されているのは上記の係数は何でも良いという理由に加え,誤差逆伝播時に計算される微分したときに綺麗な式にするためです.
二乗平均誤差は回帰に良く用いられます.
交差エントロピー誤差
交差エントロピー誤差 (cross-entropy error) は次式で定義されます.
$$
E = – \sum_{k=1}^{n} {t_k \ \log{y_k}}
$$
交差エントロピー誤差はクラス分類に良く用いられます.
確率的勾配降下法
学習するためには重みとバイアスといったパラメータを最適化する必要がありますが,この最適な値は損失関数の値が最小値を取るときに得られます.
最適化というと,工学部などで授業でプログラミングがあった方はニュートン法を思い描きそうですが,ニュートン法は計算量が多く,ニューラルネットワークなどの最適化対象が多い問題に対しては用いられておりません(もしかしたら,計算アルゴリズムや特化型計算機の開発により未来で爆速化された場合はニュートン法やその亜種が用いられるようになるかもしれません).
そんなときに用いるのが勾配降下法 (gradient descent) です.
勾配降下法
勾配降下法は,関数の傾き(つまり勾配)が負の方向に向かって逐次移動させることにより,その関数の最小値を探索するという最適化アルゴリズムで,その点付近の関数の傾きしか必要ないので,ニュートン法に比べ計算量も少なく済みます.
かといって,その方向が本当に最小値に向かっているかということは,特に多くの次元を持つ複雑なパラメータ空間上では保証されません.
従って,移動量や収束判定条件などを考えて,繰り返し計算することが重要になってきます.
簡単に2次元空間上だとイメージとしては下図です.
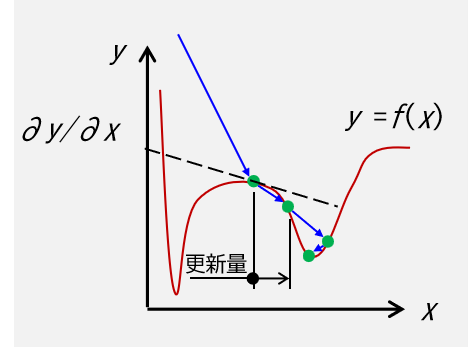
\(y = f(x)\) が勾配降下法によって最小値を求めたい対象となる関数,緑の○が繰り返し計算して更新された後の値,破線は勾配,緑の丸の \(x\) 方向成分 \(- \eta \frac{\partial f}{\partial x}\)が更新量を表します.
勾配降下法は次式で表されます.
$$
x \leftarrow x – \eta \frac{\partial f}{\partial x}
$$
ここで右辺から左辺へ向かう矢印は更新することを表していて,等号ではありません.
また \(\eta\) は学習率 (learning rate) で,1回の学習でどの程度パラメータを更新するかを制御するものです.
図の通り,繰り返し計算によって値は減少していることが示されています.
しかし,図の例で収束して至った点は,この関数の大域的な最小値でなく局所的な最小値(極小値)に陥っていることに注意が必要です.
局所的な領域に陥ることや,傾きがほとんどない平坦な領域(プラトー, plateau)で全然更新されないこと,また,学習率の設定が悪かったりするといつまでたっても収束しないことなどは良く発生します.
これらを緩和するために,次の確率的勾配降下法を用います.
確率的勾配降下法
勾配降下法で重みが更新されなくなったり局所的な最小値に陥る理由としては,その点における勾配が0に近いことや,勾配を求める対象の損失関数の形状が固定されていることに依存します.
ですので,損失関数の形状が固定されないよう,学習データの一部をランダムに取り出して学習していくミニバッチ (mini batch) 学習を取り入れる必要があります.
このミニバッチ学習を用いた勾配降下法を,ランダムにデータの一部を取り出したという意味で ”確率的” というのを頭につけた,確率的勾配降下法 (Stochastic Gradient Descent; SGD) と呼びます.
ここでミニバッチ学習の仲間としてオンライン学習とバッチ学習がありますが,オンライン学習は学習データから1つずつ選んで学習していくのに対し,バッチ学習は学習データ全体を束 (batch) の状態で一気に学習することを指します.
数式は勾配降下法と同じですが,図としては更新の度に損失関数の形状が変化していく下図のようなイメージで,そこが勾配降下法と異なる点です(図では損失関数:\(E\) と重み: \(W\) として図示しています).
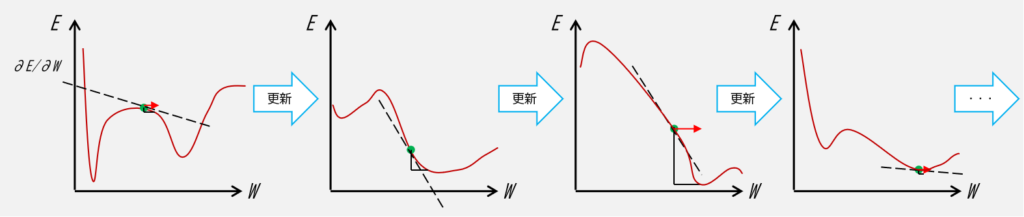
とはいえ,完全に局所解を防げるわけではなく,例えば,学習データのどのデータにおいても局所最小値が存在するような損失関数の形状となる場合は,そこに陥る場合もあります.
誤差逆伝播
誤差逆伝播 (backpropagation) は,ニューラルネットワークの順伝播計算(入力から出力へと向かう向き)で損失を算出し,この損失を今度は出力側から入力側へ逆方向に伝播させて損失を最小化するような重みを更新していくといった,ニューラルネットワークを学習させるためのアルゴリズムです.
ニューラルネットワークたらしめる肝の部分ですね.
(今まで述べてきた概念は,この誤差逆伝播で用いるために説明してきました.)
誤差逆伝播について,下図のような単純パーセプトロンで説明していきます.
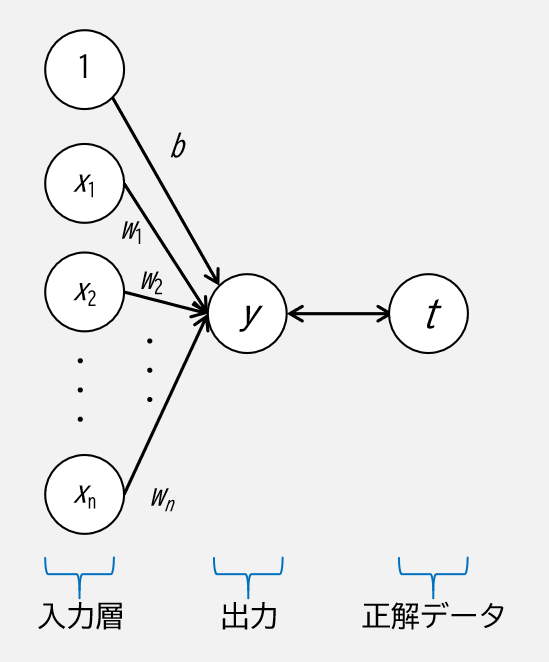
まずはニューラルネットワークの出力を求めます.
出力 \(y\) は,重みと入力の積とバイアスの和を活性化関数に通したもので,
$$
y = h(a) \\
a = b + \sum_{i=1}^{n}{w_i x_i}
$$
です.
今回の活性化関数 \(h\) は,次のシグモイド関数とします.
$$
h(a) = \frac{1}{1 + \exp{(-a)}}
$$
次に出力と正解データの損失を損失関数で求めます.
今回は損失関数 \(E\) を次式の二乗平均誤差とします.
$$
E = \frac{1}{2} (y – t)^2
$$
これで順伝播の計算は終わりで,逆伝播計算に移ります.
重みを(確率的)勾配降下法で更新していって最小化するので,損失を下げるために損失に対する重みの偏微分 \(\frac{\partial E}{\partial w_i} \) を計算していきます.
これをどうやって計算するかというと,「合成関数の微分はそれぞれの導関数の積で与えられる」という連鎖律 (chain rule) を用いて求めることができます.
今,損失 \(E\) は出力 \(y\) の関数なので,
$$
\frac{\partial E}{\partial w_i} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial w_i}
$$
と連鎖律より変形できます.
損失 \(E\) は先程定義しましたが,この微分を考えてみると,
$$
\frac{\partial E}{\partial y} = t – y
$$
であり,活性化関数を顕在化させた表現 \(y = h(a)\) を代入すると,
$$
\frac{\partial E}{\partial w_i} = (t – y) \frac{\partial h(a)}{\partial w_i}
$$
またまた連鎖律により \(h(a)\) を分解すると,
$$
\frac{\partial E}{\partial w_i} = (t – y) \frac{\partial h(a)}{\partial a} \frac{\partial a}{\partial w_i}
$$
となります.
ここで,活性化関数であるシグモイド関数の微分を考えてみると,
$$
\begin{align}
\frac{\partial h(a)}{\partial a} &= -1 \cdot \frac{1}{(1 + \exp{(-a)})^{2}} \cdot (- \exp{(-a)}) \\
&= \frac{1}{1 + \exp{(-a)}} \cdot \frac{\exp{(-a)}}{1 + \exp{(-a)}} \\
&= \frac{1}{1 + \exp{(-a)}} \cdot \frac{\exp{(-a)} + 1 – 1}{1 + \exp{(-a)}} \\
&= \frac{1}{1 + \exp{(-a)}} \cdot \left( 1 – \frac{1}{1 + \exp{(-a)}} \right) \\
&= h(a) \cdot (1 – h(a)) \\
&= y \cdot (1 – y)
\end{align}
$$
ということで,シグモイド関数は自分自身で書きあらわすことができます.
また,\(a\) における \(w_i\) の偏微分は,
$$
\begin{align}
& a = b + \sum_{i=1}^{n}{w_i x_i} \\
& \rightarrow \frac{\partial a}{\partial w_i} = x_i
\end{align}
$$
なので,これらを \(\frac{\partial E}{\partial w_i}\) の式に代入すると,
$$
\begin{align}
\frac{\partial E}{\partial w_i} &= (t – y) \ y \ (1 – y) \ x_i\\
&= x_i \ (t – y) \ (1 – y) \ y
\end{align}
$$
以上より,(確率的)勾配降下法の式に代入すると,
$$
w_i \leftarrow w_i – \eta \ x_i \ (t – y) \ (1 – y) \ y
$$
というように,重みが更新されていきます.
この式を見ると重みの更新に必要なものは,ハイパーパラメータの学習率,ネットワークの入力/出力,正解データのみで更新でき,しかもそれが簡単な差と積のみで簡単に表現できてしまいました.
ここで注意として,導かれた重み更新の式ですが,以下の条件で制約があったことを断っておきます.
- 単純パーセプトロン
- 活性化関数にシグモイド関数を適用
- 損失関数に二乗平均誤差を適用
すなわち,活性化関数が ReLU 関数を用いたり,損失関数に交差エントロピー誤差を用いるような場合では,また数式を立て直す必要があります.
(現代のようにディープラーニングのフレームワーク(次回の記事にて記載)が無いような数年前では,自力で数式を導出して C / C++ などで自前実装されていたそうです.便利な時代になりました.)
想像に難くないのですが,これが多層パーセプトロンになると,数式はもっと複雑になりますが,当該記事では割愛いたします.
次の参考図書が色のあるイラスト付き,かつ,きちんと数式が書かれているのでオススメです.
コード実装
API
ディープラーニング用のライブラリも色々あるのですが,今回は全結合層のみ扱うこととし,機械学習ライブラリの scikit-learn で十分なのでこれを使います.
全結合層のニューラルネットワークについては sklearn.neural_network に収録されており,クラス分類であれば sklearn.neural_network.MLPClassifier,回帰であれば sklearn.neural_network.MLPRegressor を用います.
(scikit-learn 的には,MLP はニューラルネットワークに含まれるという認識のようですね.)
API は以下です.
MLPClassifier (https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPClassifier.html)
class sklearn.neural_network.MLPClassifier(hidden_layer_sizes=(100,), activation='relu', *, solver='adam', alpha=0.0001, batch_size='auto', learning_rate='constant', learning_rate_init=0.001, power_t=0.5, max_iter=200, shuffle=True, random_state=None, tol=0.0001, verbose=False, warm_start=False, momentum=0.9, nesterovs_momentum=True, early_stopping=False, validation_fraction=0.1, beta_1=0.9, beta_2=0.999, epsilon=1e-08, n_iter_no_change=10, max_fun=15000)MLPRegressor (https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPRegressor.html)
class sklearn.neural_network.MLPRegressor(hidden_layer_sizes=(100,), activation='relu', *, solver='adam', alpha=0.0001, batch_size='auto', learning_rate='constant', learning_rate_init=0.001, power_t=0.5, max_iter=200, shuffle=True, random_state=None, tol=0.0001, verbose=False, warm_start=False, momentum=0.9, nesterovs_momentum=True, early_stopping=False, validation_fraction=0.1, beta_1=0.9, beta_2=0.999, epsilon=1e-08, n_iter_no_change=10, max_fun=15000)両者引数は同じなので,まとめて以下に引数の一覧表を示します.
| パラメータ名 | 初期値 | 型/取りうる値 | 説明 |
|---|---|---|---|
| hidden_layer_sizes | (100,) | list, tuple | 隠れ層の層ごとのニューロンの数を指定します.例えば隠れ層が2層でニューロンをそれぞれ第1層:20個,第2層10個としたい場合は (20, 10) と指定します. |
| activation | "relu" | "identity", "logistic", "tanh", "relu" | 隠れ層の活性化関数を指定します."identity": そのままの値 f(x)=x, "logistic": シグモイド関数 f(x)=1/(1+exp(-x)), "tanh": hyperbolic tan f(x)=tanh(x), "relu": ReLU 関数 f(x)=maximum(0, x) から選ぶことができます. |
| solver | "adam" | "lbfgs", "sgd", "adam" | 最適化関数を指定します."lbfgs": 疑似ニュートン法, "sgd": 確率的勾配降下法, "adam": Adaptive momentum から選ぶことができます. |
| alpha | 0.0001 | float | L2正則化項の強さを指定します. |
| batch_size | "auto" | int, "auto" | ミニバッチに用いるデータ数を指定します."auto" の場合 batch_size=min(200, n_samples) にて計算されます. |
| learning_rate | "constant" | "constant", "invscaling", "adaptive" | このパラメータは solver="sgd" の場合にのみ使用されます.重み更新に用いる学習率のスケジューリングを行います."constant" は終始一定,"invscaling" は learning_rate_init / pow(t, power_t) で計算されるような時間ステップ t ごとに学習率を徐々に減少させます."adaptive" は,学習時における損失が減少し続ける場合は学習率一定にし,複数回連続して tol 以上で損失の減少が見られない,もしくは,early_stopping=True の場合に少なくとも tol だけ損失を減少することを失敗する度に,学習率が 1/5 倍され小さくなっていきます. |
| learning_rate_init | 0.001 | float | 学習率の初期値を指定します. |
| power_t | 0.5 | float | learning_rate="invscaling" かつ solver="sgd" のときに,学習率の計算に使用される値. |
| max_iter | 200 | int | 繰り返し計算させる回数の最大値で,tol 未満になるかこの値に至るまで計算されます.俗に言う epoch と同一です. |
| shuffle | True | bool | solver="sgd", "adam" の際に,各繰り返し計算ごとにデータをシャッフルします. |
| random_state | None | int, None | 乱数シード値を指定します. |
| tol | 0.0001 | float | 収束判定に用いる許容値を指定します.損失もしくはスコアが n_iter_no_change で tol 未満の損失減少幅の場合,learning_rate="adaptive" に設定されていない限り収束したとみなされ,学習はそこで打ち切ります. |
| verbose | False | bool | 計算の進捗状況を標準出力するかどうかを制御します. |
| warm_start | False | bool | 学習する際に学習の途中からか,初めからかを指定します. |
| momentum | 0.9 | float (0~1) | 勾配降下法の更新に用いられるモーメントを指定します.solver="sgd" の場合にのみ使用されます. |
| nesterovs_momentum | True | bool | Nesterov の加速勾配降下法を用いるかどうかを制御します.solver="sgd" かつ momentum > 0 の場合にのみ使用されます. |
| early_stopping | False | bool | 学習の早期打ち切りを使用するかを制御します.True にすると学習データの 10 % が検証用データ用に自動的に分けられ,その検証データのスコアが n_iter_no_change 回連続で損失減少幅が tol 未満の際に学習が打ち切られます. |
| validation_fraction | 0.1 | float (0~1) | early_stoppling=True のときにのみ使用され,早期打ち切りに用いる検証データの割合を制御します. |
| beta_1 | 0.9 | float (0<=x<1) | solver="adam" のときのみに使用される,Adam の最初のモーメントに用いられる値. |
| beta_2 | 0.999 | float (0<=x<1) | solver="adam" のときのみに使用される,Adam の2つめのモーメントに用いられる値. |
| epsilon | 1e-08 | float | solver="adam" のときのみに使用される,計算安定性を制御する値. |
| n_iter_no_change | 10 | int | solver="sgd", "adam" のときのみに使用される,損失が tol に満たない場合の最大の epoch 数. |
| max_fun | 15000 | int | solver="lbfgs" のときに使用される,損失関数を呼び出す回数の最大値. |
パラメータでは損失関数を設定するところがありませんが,MLPClassifier は log-loss (Softmax) 関数,MLPRegressor は二乗平均誤差を用いています.
使用例
それでは使っていきましょう.
今回もフリーのデータセットで有名なアヤメ(花)の品種分類データセットの “iris dataset” (https://archive.ics.uci.edu/ml/datasets/Iris) を用います.
このデータセットについて,説明変数が “sepal_length”: がく片の長さ,”sepal_width”: がく片の幅,”petal_length”: 花びらの長さ,”petal_width”: 花びらの幅,目的変数が “species”: アヤメの品種名 とした 150 個のデータで構成されています.
まずは,以下のように,データを読み込みます(インストールされていない場合は “pip install scikit-learn, seaborn” を実行ください).
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
iris = sns.load_dataset(name="iris")
print(iris)
sns.pairplot(data=iris, hue="species")
plt.show()
# sepal_length sepal_width petal_length petal_width species
# 0 5.1 3.5 1.4 0.2 setosa
# 1 4.9 3.0 1.4 0.2 setosa
# 2 4.7 3.2 1.3 0.2 setosa
# 3 4.6 3.1 1.5 0.2 setosa
# 4 5.0 3.6 1.4 0.2 setosa
# .. ... ... ... ... ...
# 145 6.7 3.0 5.2 2.3 virginica
# 146 6.3 2.5 5.0 1.9 virginica
# 147 6.5 3.0 5.2 2.0 virginica
# 148 6.2 3.4 5.4 2.3 virginica
# 149 5.9 3.0 5.1 1.8 virginica
# [150 rows x 5 columns]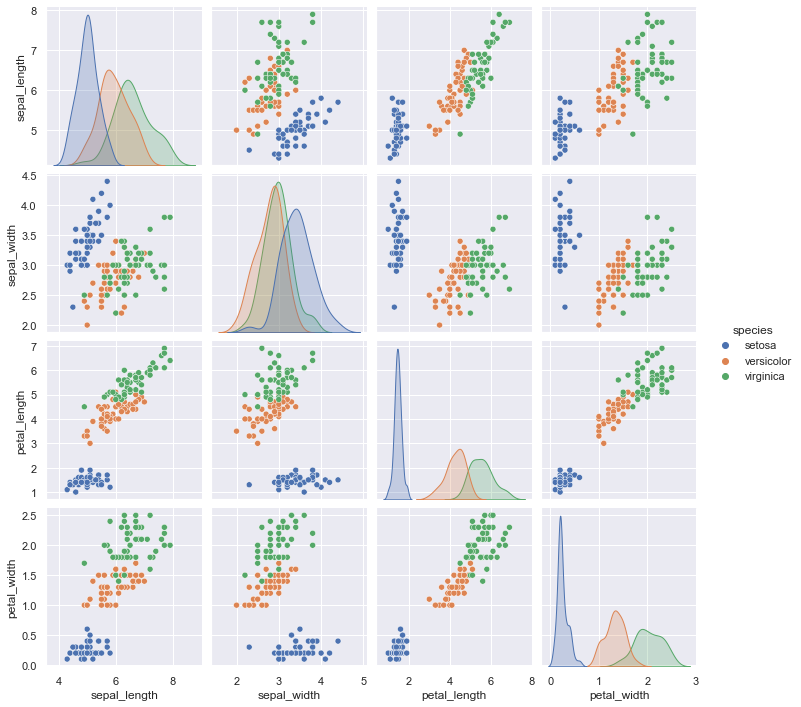
上図から,決定境界を可視化しやすいように2次元の説明変数で分類できそうなデータセットにするため,ここでは “sepal_length” と “sepal_width”,それと目的変数の “species” のみ抜き出して用います.
petal = iris[["petal_length", "petal_width", "species"]]
plt.figure(facecolor="white")
sns.scatterplot(data=petal, x="petal_length", y="petal_width", hue="species")
plt.tight_layout()
plt.show()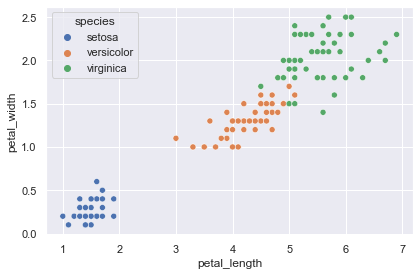
scikit-learn の学習では,ラベルは 0, 1, …, と整数にする必要があります.
このようにラベルなどのカテゴリー変数を数値に変換することをラベルエンコーディング (label encoding) と呼びます.
お手正の変換用の辞書でも構いませんが,scikit-learn にラベルエンコーディングできる関数が用意されていますので,今回は “sklearn.preprocessing.LabelEncoder” を用いて,説明変数を “x”,目的変数を “y” としておきます.
さらに,ついでに学習用と検証用でデータ分割しておきます.
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
# 説明変数のカラムだけ抜き出す
x = petal[[v for v in petal.columns if str(v).startswith("petal_")]]
# "species" カラムをラベルエンコーディングして y と置く
encoder = LabelEncoder()
encoder.fit(petal["species"])
y = encoder.transform(petal["species"])
# データ分割
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.2, shuffle=True, random_state=0, stratify=y
)
print(y_train[:10])
# [0 0 0 0 1 0 2 2 1 2]目的変数はクラスなので MLPClassifierを用います.
また,パラメータについては solver=”sgd”, random_state=0 とし,その他はデフォルトで計算してみましょう.
使い方は scikit-learn なので,いつも通り「モデル定義」→「fit メソッドで学習」→「predict メソッドで推論」です.
from sklearn import neural_network
model = neural_network.MLPClassifier(solver="sgd", random_state=0)
model.fit(x_train, y_train)
print(model.predict(x_train)[:10])
# ConvergenceWarning: Stochastic Optimizer: Maximum iterations (200) reached and the optimization hasn't converged yet.
# [0 0 0 0 2 0 2 2 2 2]先程の出力と見比べると所々間違っていますね.
そして,「収束していない」というエラーも出てきました.
とりあえず学習はできていそうですので.習に用いていない検証用データセットについても推論し,認識精度を算出してみます.
from sklearn.metrics import accuracy_score
y_pred = model.predict(x_test)
print(f"正解ラベル: {y_test}")
print(f"推論結果: {y_pred}")
print(accuracy_score(y_true=y_test, y_pred=y_pred))
# 正解ラベル: [0 1 0 2 0 1 2 0 0 1 2 1 1 2 1 2 2 1 1 0 0 2 2 2 0 1 1 2 0 0]
# 推論結果: [0 2 0 2 0 2 2 0 0 2 2 2 2 2 2 2 2 2 2 0 0 2 2 2 0 2 2 2 0 0]
# 0.6666666666666666検証用データセットについて認識精度は 66.7 % と低めの推論結果となりました.
一方,決定木 (https://slash-z.com/decision-tree/) では 96.7 % の認識精度でした.
実際,どのような決定境界が得られたのか図示してみましょう.
以下の関数は,インプレス出版の「[第2版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践」 (https://book.impress.co.jp/books/1120101017 :リンクは第3版) の p.32 n “plot_decision_regions” 関数を参考にしました.
import warnings
from matplotlib.colors import ListedColormap
def plot_decision_regions(
x: np.ndarray,
y: np.ndarray,
model,
resolution: float = 0.02,
xlabel: str = None,
ylabel: str = None,
figsize: tuple = (6, 5),
encoder: LabelEncoder = None,
) -> None:
# キャスト
x = np.array(x)
y = np.array(y)
# マーカーとカラーマップの準備
markers = ("s", "x", "o", "^", "v")
colors = ("red", "blue", "lightgreen", "gray", "cyan")
cmap = ListedColormap(colors=colors[:len(np.unique(y))])
# 決定境界のプロット
x1_min, x1_max = x[:, 0].min() - 1, x[:, 0].max() + 1
x2_min, x2_max = x[:, 1].min() - 1, x[:, 1].max() + 1
# グリッドポイントの生成
xx1, xx2 = np.meshgrid(
np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution),
)
# 各特徴量を1次元配列に変換して予測を実行
z = model.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
# 予測結果を元のグリッドポイントのデータサイズに変換
z = z.reshape(xx1.shape)
# プロット
plt.figure(figsize=figsize)
# グリッドポイントの等高線のプロット
plt.contourf(xx1, xx2, z, alpha=0.3, cmap=cmap)
# 軸の範囲の設定
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# クラスごとにサンプルをプロット
for idx, label in enumerate(np.unique(y)):
if encoder:
label_name = encoder.inverse_transform([label])[0]
else:
label_name = label
with warnings.catch_warnings():
warnings.simplefilter('ignore')
plt.scatter(
x=x[y==label, 0],
y=x[y==label, 1],
alpha=0.8,
c=colors[idx],
marker=markers[idx],
label=label_name,
edgecolor="black",
)
if xlabel:
plt.xlabel(xlabel)
if ylabel:
plt.ylabel(ylabel)
plt.legend(loc="best")
plt.tight_layout()
plt.show()
plt.clf()
plt.close()print(f"accuracy score: {accuracy_score(y_true=y, y_pred=model.predict(x)):.6f}")
plot_decision_regions(
x=x, y=y, model=model, xlabel="petal_length", ylabel="petal_width", encoder=encoder
)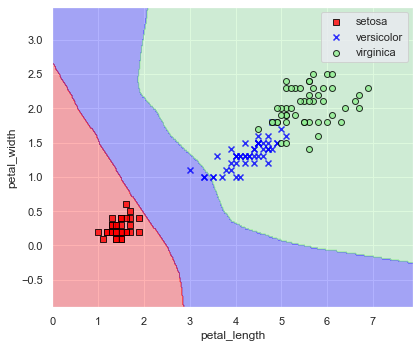
分かっていることでしたが決定境界を見てもあまりうまく行っていませんね.
「収束できてない」というエラーからも分かる通り,パラメータ設定が良くありませんでした.
上記について,隠れ層の設計 (hidden_layer_sizes),繰り返し回数 (max_iter),などを変えて精度改善を試みてみましょう.
次は精度改善の例です
model = neural_network.MLPClassifier(
hidden_layer_sizes=(64, 32, 16),
solver="sgd",
max_iter=500, random_state=0,
)
model.fit(x_train, y_train)
print(f"accuracy score: {accuracy_score(y_true=y, y_pred=model.predict(x)):.6f}")
plot_decision_regions(
x=x, y=y, model=model, xlabel="petal_length", ylabel="petal_width", encoder=encoder
)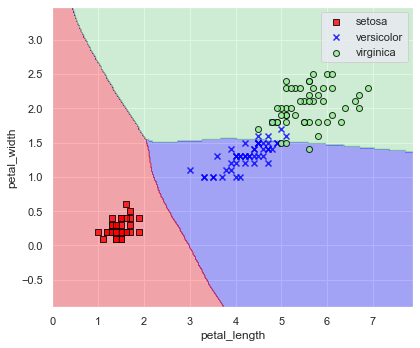
SVM の結果や決定木の結果と見比べると,そう来たかって感じですよね.
今回はきちんと分類できている感じがあります.
お気づきの方もいらっしゃるでしょうが,ニューラルネットワークは自由に設計できる反面,ハイパーパラメータだらけです.
線形分離が不可能なパターンについても見てみましょう.
rng = np.random.default_rng(seed=0)
size = 300
# 説明変数
x = rng.normal(size=size*2).reshape((size, 2))
# 目的変数
y = x[:,0]*x[:,1] > 0
fig = plt.figure(facecolor="white")
ax = plt.axes(aspect="equal")
ax.scatter(x[:, 0], x[:, 1], c=y, cmap="coolwarm_r")
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
fig.tight_layout()
plt.show()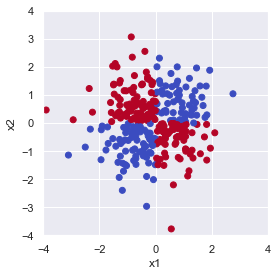
上図は \(x_1 \times x_2\) が 0 より大きくなる点(第1,3象限)を True で青, 0 以下になる点(第2,4象限)を False で赤としてプロットしています.
とりあえずパラメータについては solver=”sgd”, random_state=0 とし,その他はデフォルトで計算してみましょう.
model = neural_network.MLPClassifier(solver="sgd", random_state=0)
model.fit(x, y)
print(f"accuracy score: {accuracy_score(y_true=y, y_pred=model.predict(x)):.6f}")
plot_decision_regions(x=x, y=y, model=model, xlabel="x1", ylabel="x2")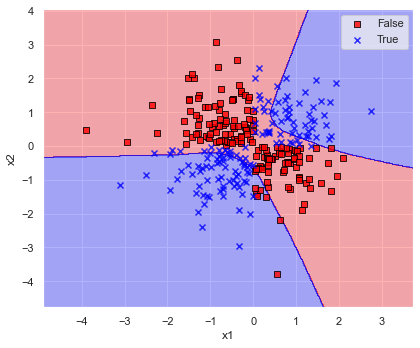
では,パラメータ調整して改良しましょう.
model = neural_network.MLPClassifier(
hidden_layer_sizes=(64, 32, 16),
solver="sgd",
max_iter=500,
random_state=0,
)
model.fit(x, y)
print(f"accuracy score: {accuracy_score(y_true=y, y_pred=model.predict(x)):.6f}")
plot_decision_regions(x=x, y=y, model=model, xlabel="x1", ylabel="x2")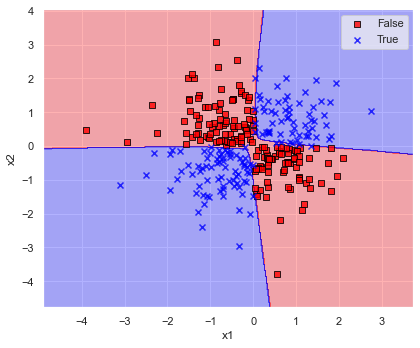
データをだいたい4つの象限で分けることができました.
演習問題
Q1. ワインデータセットについて,以下を参照して,目的変数であるワインの等級を予測してみましょう.
- データ分割は train_test_split にて行い,学習用データは全データの 90 %,データのシャッフルは True としてください(結果に再現性を持たせたい場合は,引数 random_state に任意の数を設定してください)
- データは,以下のコードにて読み込むことができます(データの説明はこちら:https://slash-z.com/matplotlib-first-step/)
from sklearn.datasets import load_wine
df_x, df_y = load_wine(return_X_y=True, as_frame=True)- scikit-learn を用いて分類問題における認識精度を確認するには,以下のようにして算出が可能です.
from sklearn.metrics import accuracy_score
print(accuracy_score(y_true, y_pred))Q2. カリフォルニア住宅価格データセットについて,以下の手順を参考に住宅価格を予測してみましょう.
- 次のコードでデータ読み込み,学習用/検証用にデータを分割します.
from sklearn.datasets import fetch_california_housing
df_x, df_y = fetch_california_housing(return_X_y=True, as_frame=True)
x_train, x_test, y_train, y_test = train_test_split(
df_x, df_y, test_size=0.25, shuffle=True, random_state=0,
)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)- 学習用データ (x_train, y_train) のみを学習し,検証用データ x_test について住宅価格を予測しましょう.
- 上記で予測した住宅価格について,正解の値との絶対平均誤差を算出してみましょう.
以下のコードにて絶対平均誤差が算出できます.
ここで,y_true は正解データの y_test,y_pred には x_test に対するモデルの推論結果を代入してください.
from sklearn.metrics import mean_absolute_error
print(mean_absolute_error(y_true, y_pred))Q3. カルフォルニア大学アーバイン校(UCI)が提供している,手書き数字のデータセット (API: https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_digits.html) について,何の数字かを認識してみましょう.データ読み込みは以下のコードを実行します.
from sklearn.datasets import load_digits
# データ読み込み
x, y = load_digits(return_X_y=True)演習問題の解答
Q1. ワインデータセットについて,目的変数であるワインの等級を予測してみましょう.
import numpy as np
import pandas as pd
from sklearn.datasets import load_wine
from sklearn.metrics import accuracy_score
from sklearn import neural_network
from sklearn.model_selection import train_test_split
# データ読み込み
df_x, df_y = load_wine(return_X_y=True, as_frame=True)
# データ分割
x_train, x_test, y_train, y_test = train_test_split(
df_x, df_y, test_size=0.1, shuffle=True, random_state=0, stratify=df_y
)# 学習/推論
model = neural_network.MLPClassifier(solver="sgd", random_state=0)
model.fit(x_train, y_train)
pred = model.predict(df_x)
# 分類精度算出
print(accuracy_score(y_true=df_y, y_pred=pred))
# 0.33146067415730335model = neural_network.MLPClassifier(solver="sgd", hidden_layer_sizes=(512, 256, 64), random_state=0)
model.fit(x_train, y_train)
pred = model.predict(df_x)
print(accuracy_score(y_true=df_y, y_pred=pred))
# 0.398876404494382model = neural_network.MLPClassifier(solver="adam", random_state=0)
model.fit(x_train, y_train)
pred = model.predict(df_x)
print(accuracy_score(y_true=df_y, y_pred=pred))
# 0.9213483146067416Q2. カリフォルニア住宅価格データセットについて,住宅価格を予測してみましょう.
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_absolute_error
# データ読み込み/分割
df_x, df_y = fetch_california_housing(return_X_y=True, as_frame=True)
df_x = (df_x - df_x.min()) / (df_x.max() - df_x.min())
x_train, x_test, y_train, y_test = train_test_split(
df_x, df_y, test_size=0.25, shuffle=True, random_state=0,
)model = neural_network.MLPRegressor(solver="sgd", random_state=0)
model.fit(x_train, y_train)
pred = model.predict(x_test)
print(mean_absolute_error(y_true=y_test, y_pred=pred))
# 0.5163586152066993model = neural_network.MLPRegressor(solver="adam", random_state=0)
model.fit(x_train, y_train)
pred = model.predict(x_test)
print(mean_absolute_error(y_true=y_test, y_pred=pred))
# 0.4389179166459008Q3. カルフォルニア大学アーバイン校(UCI)が提供している,手書き数字のデータセット (API: https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_digits.html) について,何の数字かを認識してみましょう.
from sklearn.datasets import load_digits
# データ読み込み
x, y = load_digits(return_X_y=True)
print(x.shape, y.shape)import matplotlib.pyplot as plt
plt.imshow(x[0].reshape((8,8)), cmap="gray")
plt.title(f"label: {y[0]}")
plt.show()
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.1, shuffle=True, random_state=0, stratify=y
)
model = neural_network.MLPClassifier(solver="sgd", random_state=0)
model.fit(x_train, y_train)
pred = model.predict(x)
print(accuracy_score(y_true=y, y_pred=pred))
# 0.9955481357818586Deep Learning の勉強でおすすめの本
「イラストで学ぶディープラーニング」
「ゼロから作る Deep Learning ①」




コメント