ディープラーニングが流行ったのは,2010年から始まった大規模画像認識コンペティションの ILSVRC (ImageNet Large Scale Visual Recognition Challenge) において,2012年大会の ImageNet データセット(画像枚数100万枚超,1000クラス分類)に対する画像認識で,AlexNet と呼ばれるディープラーニングを用いた画像認識モデルがトップエラー5という指標で昨年の記録を 25.8 % → 16.4 % と大幅更新した結果,AI/ディープラーニングのブームが起こりました(これ以前は画像から SIFT 特徴量などを抽出し,それを SVM などの機械学習で分類していたそうです).
更には,これ以降のコンペでもディープラーニングを用いたモデルによって毎年認識精度が更新されていき,2015年の ResNet では人間の認識精度である 5.1 % を下回る 3.5 % を叩き出しました.
その火付け役が,この畳み込みニューラルネットワーク (Convolutional Neural Network; CNN) です.
畳み込みニューラルネットワークは,畳み込み層やプーリング層によって特徴量を抽出していくネットワーク構造で,特に画像に対するタスクである画像認識:画像一枚に対するクラス一つを返すタスク,物体検出:画像の中の物体をバンディングボックスで囲んで出力するタスク,セグメンテーション:画像ピクセル毎にクラス分類を行うタスク,などで多様な発展を遂げています.
(最近は Transformer の出現/発展により,CNN による様々な記録が塗り替えられそうです.)
今回は,畳み込みニューラルネットワークの処理について,ディープラーニングのフレームワークの一つの TensorFlow による実装とともに紹介していきます.
当該記事のコードは次の github にも記載しています.
畳み込みニューラルネットワークの例
中身の説明に入る前に,畳み込みニューラルネットワークの具体例を下図で示します.
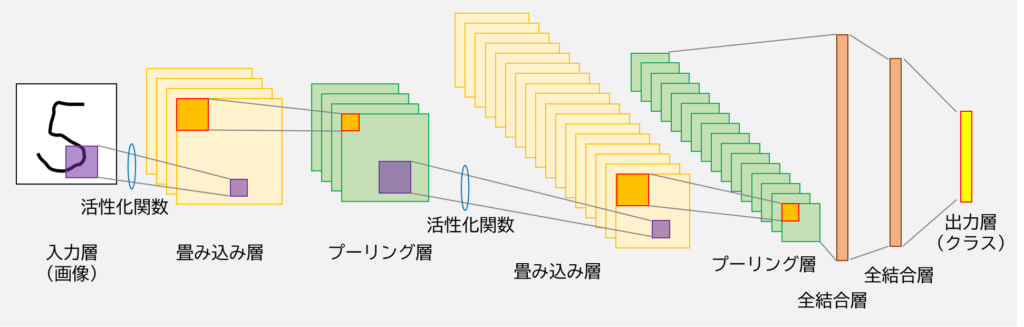
ディープラーニングの回 (https://slash-z.com/deep-learning/) では基本的には全結合層のみでしたが,CNN では畳み込み層とプーリング層が追加されました.
全結合層は層どうしのニューロンが全て繋がり合っていましたが,縦・横といった情報がある画像を認識する場合でも問答無用に平坦化するため,近い画素や遠い画素といった位置情報に関して,層の設計としてはイマイチでした.
この点を CNN は畳み込み層とプーリング層によって,上手いこと位置情報を関連させて特徴量抽出することができます.
それでは,両者の機能について見ていきましょう.
畳み込み層
畳み込み層 (convolutional layer) はデータのいち部をフィルタを通して畳み込み演算することにより,出力である特徴マップ (feature map) を得るという層です.
CNN の学習においては,特徴量抽出に関係してくるフィルターの値(≒画素値に対する重み)が更新されていきます.
畳み込み層における固有のパラメータとしては,フィルター(filter,カーネル (kernel) と呼ばれることもある)の縦横のサイズ,フィルターのずらし量を表すストライド (stride),元画像からフィルターをはみ出させて計算させるときに値を埋めるかどうかを制御するパディング (padding) があります.
畳み込み層の演算について,イメージは下図です.
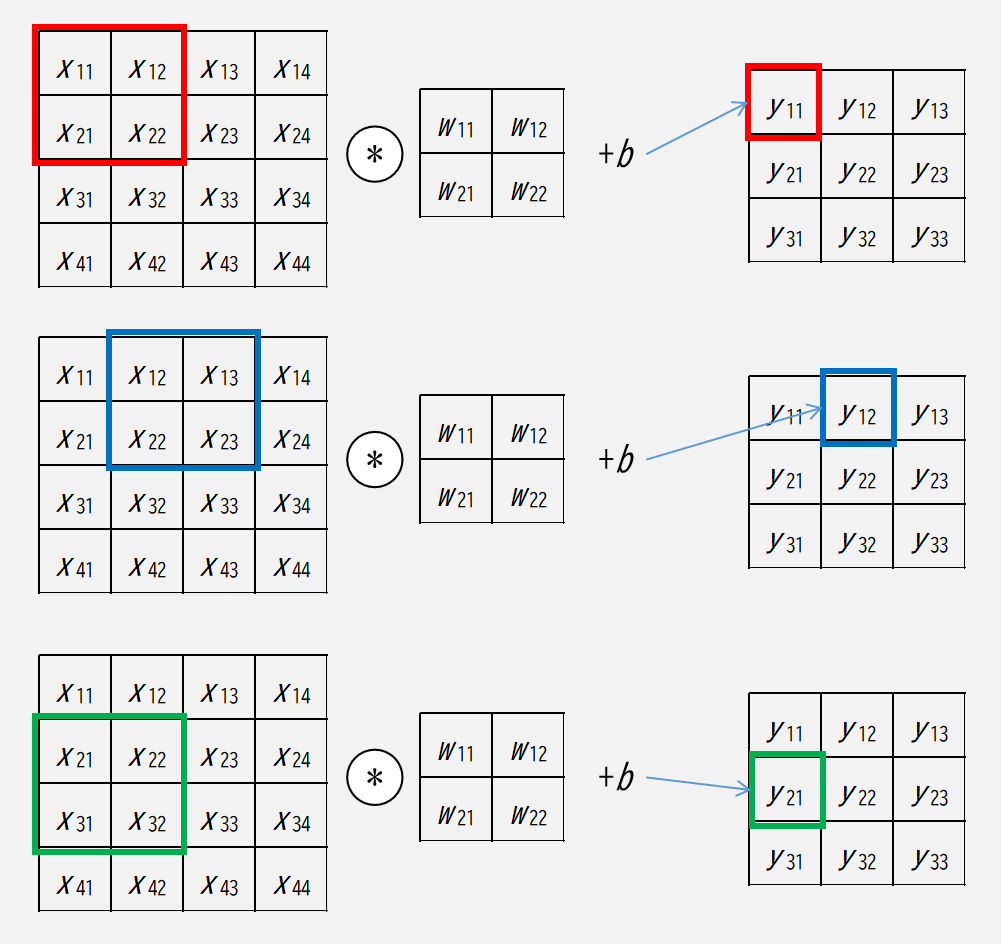
ここで,\(x\) は畳み込み層への入力,\(w_?\) はフィルター(各要素が重み),\(b\) はバイアス,\(y\) は畳み込み層の出力を表します.
また,○の中の \(\ast\) (wordpress の latex で \circledast が適用されないので以降 \(\ast\) とする)は畳み込み演算で,行列 \(A = \{a_{ij}\}, \ B = \{b_{ij}\}\) に対し,
$$
A \ast B = \sum_{i,j}{a_{ij} b_{ij}}
$$
を表します.
すなわち \(y_{11}, \ y_{12}, \ y_{21}\) は,
$$
y_{11} = w_{11} x_{11} + w_{12} x_{12} + w_{21} x_{21} + w_{22} x_{22} + b \\
y_{12} = w_{12} x_{12} + w_{13} x_{13} + w_{22} x_{22} + w_{23} x_{23} + b \\
y_{21} = w_{21} x_{21} + w_{22} x_{22} + w_{31} x_{31} + w_{32} x_{32} + b
$$
です.
ストライドとパディングを図で表すと以下です.
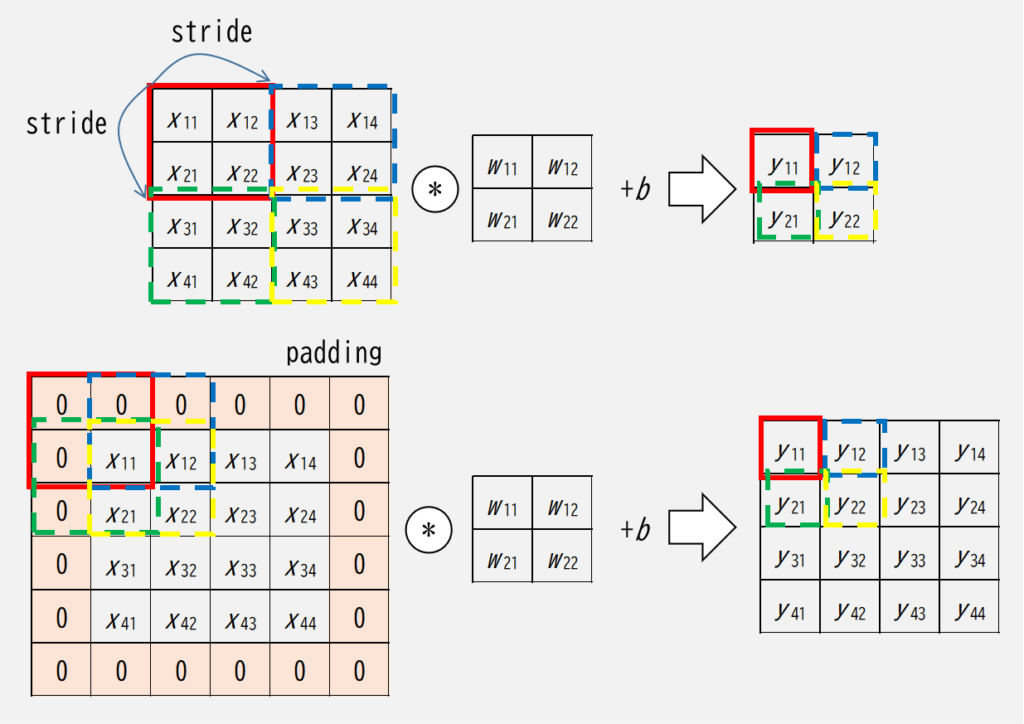
このとおり,ストライドとパディングは出力サイズの形状に影響を及ぼします.
畳み込み層の出力の形状(高さと幅)は次式によって計算できます.
$$
h_O = \frac{h_I + 2 p – h_F}{s} + 1 \\
w_O = \frac{w_I + 2 p – w_F}{s} + 1
$$
ここで,\(h\) は画像の高さ,\(w\) は画像の幅,\(I\) は入力データ,\(O\) は出力データ,\(F\) はフィルターを表します.
TensorFlow (Functional API)で実装する場合は,以下のように tensorflow.keras.layers.Conv2D (https://www.tensorflow.org/api_docs/python/tf/keras/layers/Conv2D) を用います.
以下,from keras import layers と事前にインポートしていることを前提とします.
x = layers.Conv2D(
filters=filters,
kernel_size=kernel_size,
strides=(1, 1),
padding='valid',
kernel_initializer='glorot_uniform',
*,
)(x)ここで,filters はフィルター枚数,kernel_size はフィルターのサイズ(例えば 3×3 のフィルターならば kernel_size=(3, 3)),strides はストライド(例えば縦横両方に 2 ずつならば strides=(2, 2)),padding はパディングで “valid” ならパディングなし/”same” ならパディングあり,kernel_initializer は層の重みの初期値 (https://slash-z.com/deep-learning/#toc2) を指定することができます.
プーリング層
プーリング層 (pooling layer) は,入力画像の高さと幅を小さくして,情報を集約していく処理を行う層です.
この層で設計するものとしては,入力画像に対してプーリングを行う高さと幅のプールサイズ,ストライド,パディング,それとプーリング処理方法です.
イメージとしては下図です.

プーリング処理方法は,代表的には,最大値プーリングと平均値プーリングの2種類があります(中身は名称の通りです).
最大値プーリングは,例えば次式で与えられます.
$$
y_{11} = \max{(x_{11}, \ x_{12}, \ x_{21}, \ x_{22})} \\
y_{12} = \max{(x_{12}, \ x_{13}, \ x_{22}, \ x_{23})}
$$
一方,平均値プーリングは,例えば次式で与えられます.
$$
y_{11} = \frac{1}{4} \ (x_{11} + x_{12} + x_{21} + x_{22}) \\
y_{12} = \frac{1}{4} \ (x_{12} + x_{13} + x_{22} + x_{23})
$$
上記式の通り,プーリング層において学習が必要なパラメータはありません.
TensorFlow では,tf.keras.layers.AveragePooling2D (https://www.tensorflow.org/api_docs/python/tf/keras/layers/AveragePooling2D) / MaxPool2D (https://www.tensorflow.org/api_docs/python/tf/keras/layers/MaxPool2D) を用います.
x = layers.AveragePooling2D(
pool_size=(2, 2),
strides=None,
padding='valid',
*,
)(x)
x = layers.MaxPool2D(
pool_size=(2, 2),
strides=None,
padding='valid',
*,
)(x)ここで,pool_size はプールサイズを表します.
Global Average Pooling 層
Global Average Pooling 層 (GAP) は,入力となる複数の特徴マップを一つの特徴マップに集約し,平坦化して出力します.
集約する方法は,入力となる各特徴マップの同一位置の要素の平均値を,出力する特徴マップの同一位置に押し込んで,最後に平坦化します.
イメージは下図です.
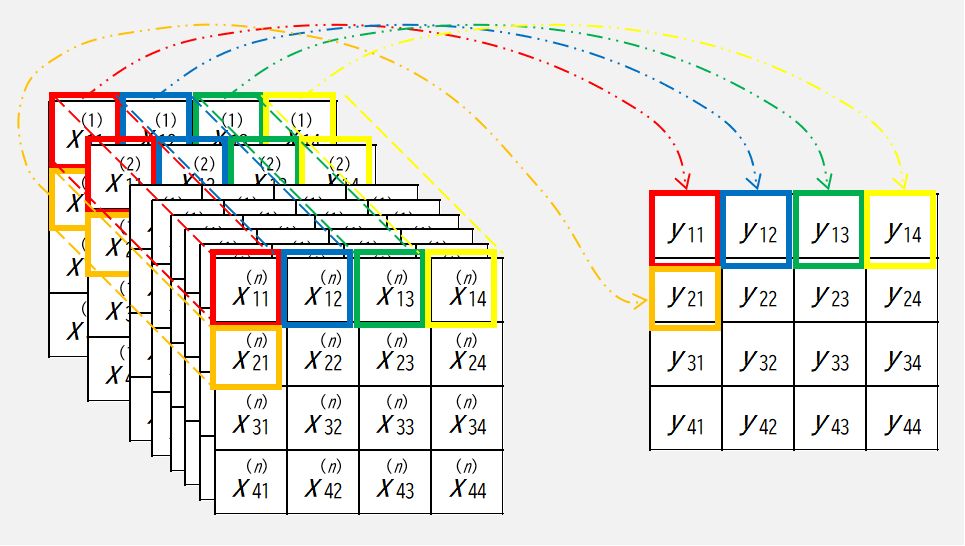
数式で表すと以下になります.
$$
y_{ij} = \frac{1}{n} \sum_{k=1}^{n}{x_{11}^{(k)}}
$$
ここで,上付きの括弧は何枚目のフィルターかを表し,GAP の出力としては,これが1次元配列に平坦化されます.
GAP は CNN に必須というわけではないのですが,例えば,CNN で全結合層につなげるときに単に平坦化すると,次に続く全結合層のニューロンの数は,最後の特徴マップの大きさと枚数の積になりますが,GAP を用いると枚数は1枚になるので,全結合層のニューロンの数,つまり学習パラメータを大幅に削減できます.
TensorFlow では,tf.keras.layers.GlobalAveragePooling2D (https://www.tensorflow.org/api_docs/python/tf/keras/layers/GlobalAveragePooling2D) を用います.
x = layers.GlobalAveragePooling2D()(x)引数は不要です.
実践:畳み込みニューラルネットワーク
実践編です.
今回の計算はパラメータ数やデータ数が多いため結構重いので,Google Colaboratory などの GPU が使える環境を推奨します.
(Intel 第11世代 core-i5 以上であれば,少々時間がかかりますが,待てるレベルで計算できます.)
ちなみに,以下計算は Google Colab の次の GPU にて計算しました(!nvidia-smi コマンドで表示).
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 510.47.03 Driver Version: 510.47.03 CUDA Version: 11.6 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 Tesla T4 Off | 00000000:00:04.0 Off | 0 |
| N/A 44C P0 26W / 70W | 1904MiB / 15360MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
| 0 N/A N/A 4478 C 1901MiB |
+-----------------------------------------------------------------------------+ニューラルネットワークで認識対象として扱った mnist では簡単なので,今回は,トロント大学が提供する,クラス分類数 10 で 32×32 ピクセル RGB の画像データが 60000 枚(学習用:50,000 枚,テスト用:10,000 枚)からなるフリーのデータセットの CIFAR-10 (https://www.cs.toronto.edu/~kriz/cifar.html) を用いて,これに対してクラス分類してみましょう.
CIFAR-10 は,ディープラーニングで良くベンチマークとして用いられているデータセットの一つです(ちなみに,CIFAR-10 の読み方は「シーファーテン」です).
それではコードを書いていきましょう.
まずはインポート処理とデータ読み込みを行います.
CIFAR-10 は TensorFlow で読み込むことができます.
import gc
import os
import math
import time
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
from keras import layers, Model, optimizers, losses, metrics, callbacks
sns.set()
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
print(x_train.shape, y_train.shape, x_test.shape, y_test.shape)
print(x_train.dtype, y_train.dtype, x_test.dtype, y_test.dtype)
# (50000, 32, 32, 3) (50000, 1) (10000, 32, 32, 3) (10000, 1)
# uint8 uint8 uint8 uint8ラベルは 0~9 で与えられており,実際は,次のような対応です.
label_name = {
"0": "airplane",
"1": "automobile",
"2": "bird",
"3": "cat",
"4": "deer",
"5": "dog",
"6": "frog",
"7": "horse",
"8": "ship",
"9": "truck",
}どんなデータなのか可視化してみましょう.
num = 36
fig = plt.figure(figsize=(12, 10))
ax = [None] * num
for i in range(num):
ax[i] = fig.add_subplot(6, 6, i + 1)
ax[i].imshow(x_train[i])
ax[i].set_title(f"{y_train[i][0]}, {label_name[str(y_train[i][0])]}")
ax[i].grid(None)
ax[i].axis("off")
fig.tight_layout()
plt.show()
何の写真かは大体分かりますが,32×32 のデータなので結構荒くて,人間でも間違って分類しそうなものもありますね.
学習に用いるので,一旦,0~255 から 0~1 に正規化し,ついでに,クラス数も算出しておきましょう.
# 画素値を 0~255 から 0~1 に正規化
x_train = x_train.astype(np.float32) / 255.0
x_test = x_test.astype(np.float32) / 255.0
# クラス数を算出
classes = len(label_name)CNN の効果を見るために,まずは全結合層のみで計算させてみましょう.
(以下ではディープラーニングの回 (https://slash-z.com/deep-learning/) でやった知識や実装を断り無く用いていきますので,予めご了承ください.)
初めに,mnist は認識できた隠れ層が1つのニューラルネットワークで試してみます.
tf.keras.backend.clear_session()
gc.collect()
inputs = layers.Input(shape=x_train.shape[1:])
x = inputs
x = layers.Flatten()(x)
x = layers.Dense(units=64, kernel_initializer="he_normal")(x)
x = layers.ReLU()(x)
x = layers.Dense(units=classes, kernel_initializer="glorot_uniform")(x)
x = layers.Softmax()(x)
outputs = x
model = Model(inputs=inputs, outputs=outputs)
model.compile(
optimizer=optimizers.Adam(learning_rate=0.01),
loss=losses.SparseCategoricalCrossentropy(),
metrics=[metrics.SparseCategoricalAccuracy()],
)
model.summary()
t_start = time.perf_counter()
model.fit(
x=x_train,
y=y_train,
validation_data=(x_test, y_test),
batch_size=64,
epochs=10,
)
print(f"\nelapsed: {time.perf_counter() - t_start:.3f} [s]")
# elapsed: 43.034 [s]ここで学習時の出力は載せませんが,学習された方は「ダメそう」と感じていることと思われます.
学習の epoch ごとに計算された認識精度,及び,損失は,model.history に格納されています.
学習時おける認識精度や損失の epoch 推移(学習曲線)について,以下関数を定義して可視化してみましょう.
def plot_history(model):
history = model.history
epoch = np.array(history.epoch) + 1
scores = history.history
acc_train = scores["sparse_categorical_accuracy"]
acc_val = scores["val_sparse_categorical_accuracy"]
loss_train = scores["loss"]
loss_val = scores["val_loss"]
fig = plt.figure(figsize=(10, 4), facecolor="white")
ax0 = fig.add_subplot(1, 2, 1)
ax1 = fig.add_subplot(1, 2, 2)
ax0.plot(epoch, acc_train, label="train")
ax0.plot(epoch, acc_val, label="validation")
ax0.set_xlabel("epoch")
ax0.set_ylabel("accuracy")
ax0.set_ylim(-0.05, 1.05)
ax1.plot(epoch, loss_train, label="train")
ax1.plot(epoch, loss_val, label="validation")
ax1.set_xlabel("epoch")
ax1.set_ylabel("loss")
fig.tight_layout()
plt.show()plot_history(model=model)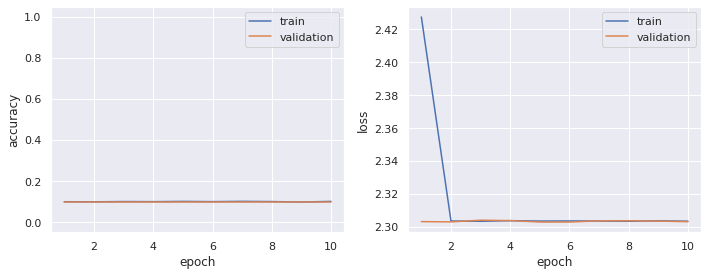
ご覧の通り,全然学習が上手くいってません.
全結合層のみでもうちょっと頑張ってみて,次は隠れ層4つの以下のバージョンでやってみましょう.
tf.keras.backend.clear_session()
gc.collect()
inputs = layers.Input(shape=x_train.shape[1:])
x = inputs
x = layers.Flatten()(x)
for i in range(4):
x = layers.Dense(units=128, kernel_initializer="he_normal")(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.Dropout(rate=0.2)(x)
x = layers.Dense(units=classes, kernel_initializer="glorot_uniform")(x)
x = layers.Softmax()(x)
outputs = x
model = Model(inputs=inputs, outputs=outputs)
model.compile(
optimizer=optimizers.Adam(learning_rate=0.01),
loss=losses.SparseCategoricalCrossentropy(),
metrics=[metrics.SparseCategoricalAccuracy()],
)
model.summary()
t_start = time.perf_counter()
model.fit(
x=x_train,
y=y_train,
validation_data=(x_test, y_test),
batch_size=64,
epochs=10,
)
print(f"\nelapsed: {time.perf_counter() - t_start:.3f} [s]")
plot_history(model=model)
# elapsed: 84.854 [s]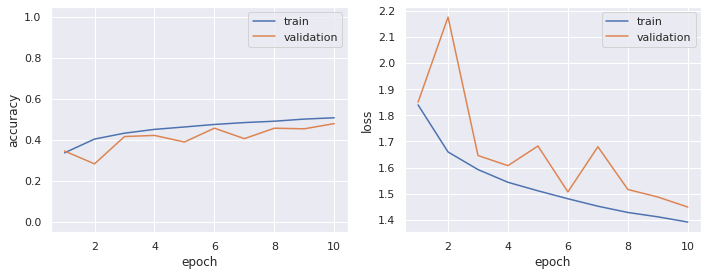
徐々に認識精度の増加/損失の減少が見られますが,少し緩やか過ぎる気もします.
それでは実際に CNN を構築して学習してみましょう.
今回は次の図のような設計とします.
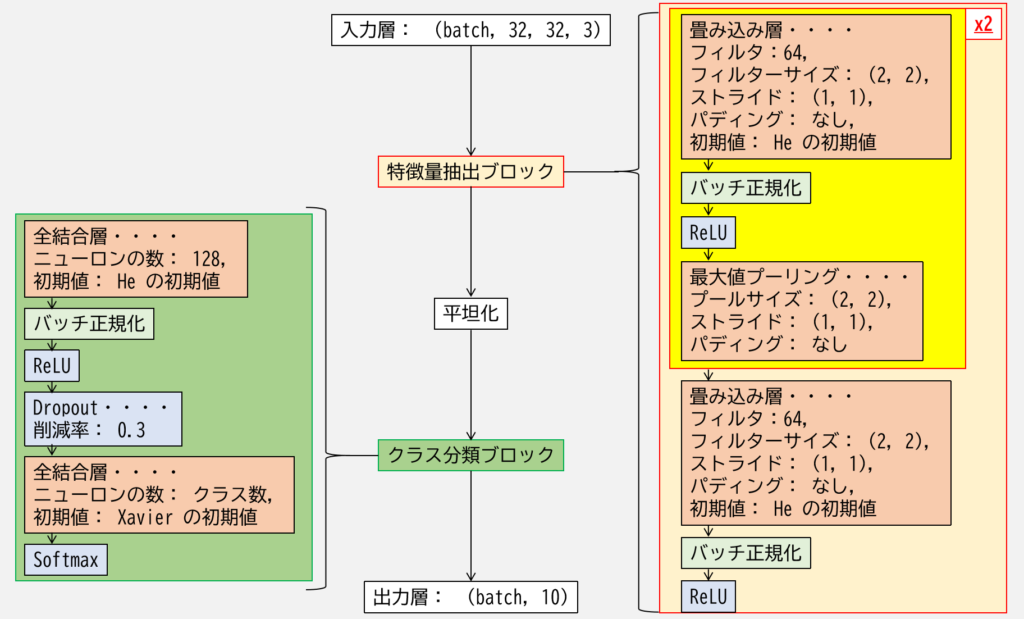
注意として,特徴量抽出ブロックの黄色い四角で囲った処理は,2回同じ処理を行わせるようにします.
tf.keras.backend.clear_session()
gc.collect()
inputs = layers.Input(shape=x_train.shape[1:])
x = inputs
for i in range(2):
x = layers.Conv2D(
filters=64,
kernel_size=(2, 2),
strides=(1, 1),
padding="valid",
kernel_initializer="he_normal",
)(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.MaxPool2D(pool_size=(2, 2), strides=(1, 1), padding="valid")(x)
x = layers.Conv2D(
filters=64,
kernel_size=(2, 2),
strides=(1, 1),
padding="valid",
kernel_initializer="he_normal",
)(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.Flatten()(x)
x = layers.Dense(units=128, kernel_initializer="he_normal")(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.Dropout(rate=0.3)(x)
x = layers.Dense(units=classes, kernel_initializer="glorot_uniform")(x)
x = layers.Softmax()(x)
outputs = x
model = Model(inputs=inputs, outputs=outputs)
model.compile(
optimizer=optimizers.Adam(learning_rate=0.01),
loss=losses.SparseCategoricalCrossentropy(),
metrics=[metrics.SparseCategoricalAccuracy()],
)
model.summary()
t_start = time.perf_counter()
model.fit(
x=x_train,
y=y_train,
validation_data=(x_test, y_test),
batch_size=64,
epochs=30,
)
print(f"\nelapsed: {time.perf_counter() - t_start:.3f} [s]")
plot_history(model=model)
# elapsed: 384.379 [s]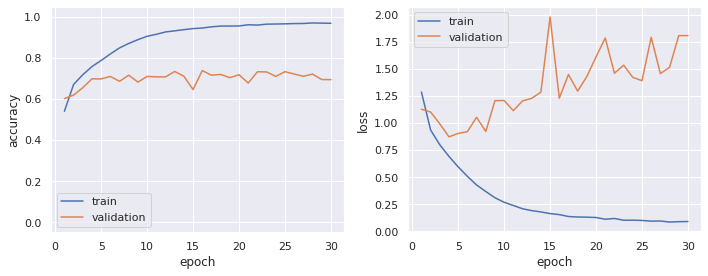
先程よりもだいぶ認識精度が上がりましたが,損失のグラフに示されるように epoch=5 以降から過学習が示唆されます.
ディープラーニングの回で紹介しました学習率スケジューラの warm up / cosine decay を適用させてみましょう.
まずは,以下で warm up / cosine decay の学習率スケジューラを定義します.
warm_up_epoch = 3
max_lr = 0.01
final_epoch = 30
def lr_scheduler(epoch: int, _: float) -> float:
if epoch <= warm_up_epoch:
scheduled_lr = epoch / warm_up_epoch * max_lr
else:
scheduled_lr = (
(
math.cos(
(epoch - warm_up_epoch) / (final_epoch - warm_up_epoch) * math.pi
)
+ 1
)
* max_lr
/ 2
)
scheduled_lr = round(scheduled_lr, ndigits=9)
return scheduled_lr次に学習時に callbacks で呼び出します.
tf.keras.backend.clear_session()
gc.collect()
inputs = layers.Input(shape=x_train.shape[1:])
x = inputs
for i in range(2):
x = layers.Conv2D(
filters=64,
kernel_size=(2, 2),
strides=(1, 1),
padding="valid",
kernel_initializer="he_normal",
)(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.MaxPool2D(pool_size=(2, 2), strides=(1, 1), padding="valid")(x)
x = layers.Conv2D(
filters=64,
kernel_size=(2, 2),
strides=(1, 1),
padding="valid",
kernel_initializer="he_normal",
)(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.Flatten()(x)
x = layers.Dense(units=128, kernel_initializer="he_normal")(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.Dropout(rate=0.3)(x)
x = layers.Dense(units=classes, kernel_initializer="glorot_uniform")(x)
x = layers.Softmax()(x)
outputs = x
model = Model(inputs=inputs, outputs=outputs)
model.compile(
optimizer=optimizers.Adam(learning_rate=0.01),
loss=losses.SparseCategoricalCrossentropy(),
metrics=[metrics.SparseCategoricalAccuracy()],
)
model.summary()
t_start = time.perf_counter()
model.fit(
x=x_train,
y=y_train,
validation_data=(x_test, y_test),
batch_size=64,
epochs=final_epoch,
callbacks=[
callbacks.LearningRateScheduler(
schedule=lr_scheduler,
verbose=0,
),
],)
print(f"\nelapsed: {time.perf_counter() - t_start:.3f} [s]")
plot_history(model=model)
# 324.688 [s]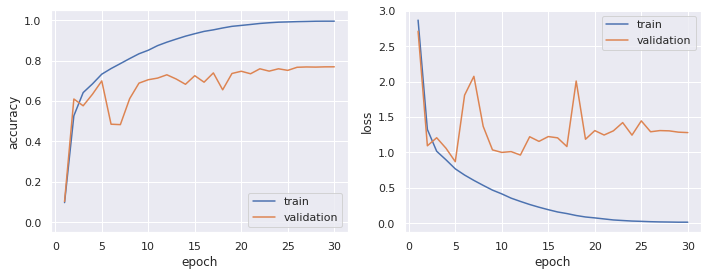
ということで,epoch 終盤の認識精度はなんとなく上昇していますが,それでもやはり,epoch=6 以降における過学習が示唆される損失の推移となりました.
こういった過学習や精度改善に対する対策として,
- データ拡張 (data augmentation) ・・・・画像データを変形や変換などを行い,画像データ数を数倍に増やす方法で,データ数が多ければ多いほど精度が良くなるディープラーニングにとっては重要な前処理
- ResNet(読み方は「レズネット」)などに用いられる skip connection を持った,更にディープな CNN の構築
が挙げられますが,両者ともそれだけで一つ記事がかけるので,今回はここまでとします.
演習問題
Q. 上記の最後に計算した CNN について,特徴量抽出ブロックとクラス分類ブロックの間の処理は平坦化処理を用いていますが,これを Global Average Pooling に変更して計算を行い,学習曲線を可視化してみましょう.
演習問題の解答
tf.keras.backend.clear_session()
gc.collect()
inputs = layers.Input(shape=x_train.shape[1:])
x = inputs
for i in range(2):
x = layers.Conv2D(
filters=64,
kernel_size=(2, 2),
strides=(1, 1),
padding="valid",
kernel_initializer="he_normal",
)(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.MaxPool2D(pool_size=(2, 2), strides=(1, 1), padding="valid")(x)
x = layers.Conv2D(
filters=64,
kernel_size=(2, 2),
strides=(1, 1),
padding="valid",
kernel_initializer="he_normal",
)(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.GlobalAveragePooling2D()(x)
x = layers.Dense(units=128, kernel_initializer="he_normal")(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.Dropout(rate=0.3)(x)
x = layers.Dense(units=classes, kernel_initializer="glorot_uniform")(x)
x = layers.Softmax()(x)
outputs = x
model = Model(inputs=inputs, outputs=outputs)
model.compile(
optimizer=optimizers.Adam(learning_rate=0.01),
loss=losses.SparseCategoricalCrossentropy(),
metrics=[metrics.SparseCategoricalAccuracy()],
)
model.summary()
t_start = time.perf_counter()
model.fit(
x=x_train,
y=y_train,
validation_data=(x_test, y_test),
batch_size=64,
epochs=final_epoch,
callbacks=[
callbacks.LearningRateScheduler(
schedule=lr_scheduler,
verbose=0,
),
],)
print(f"\nelapsed: {time.perf_counter() - t_start:.3f} [s]")
plot_history(model=model)
# elapsed: 289.915 [s]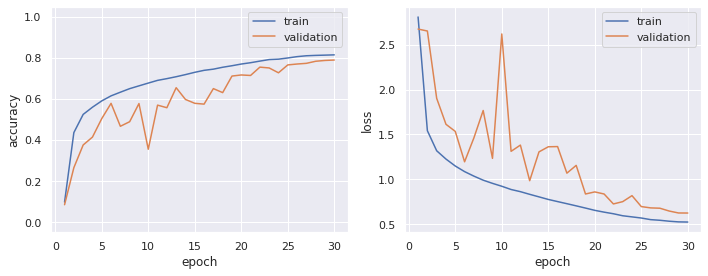
平坦化にて実装していた結果よりも過学習が抑制され,認識精度も向上しました.
また,学習パラメータ数についても,平坦化の方では 6,007,754 個あったのに対して,GAP の方では 43,978 個と圧倒的に低減できています.
このように,色々と試行錯誤が必要です.
Deep Learning の勉強でおすすめの本
「イラストで学ぶディープラーニング」
「ゼロから作る Deep Learning ①」




コメント