【自前AI講座】LASSO / Ridge 回帰 / ElasticNet の理論／数式／コード実装

ざっくりいうと LASSO / Ridge 回帰 / Elastic Net は，線形回帰モデルの損失関数に正則化項と呼ばれる項を加えた回帰モデルで，学習に用いていない未知のデータに対して線形回帰モデルよりも上手く適合させる（汎化性能を向上させる）ことができます．
項を加えるだけでモデルの汎化性能が向上できる，そんな LASSO / Ridge 回帰 / Elastic Net について今回紹介します．

コードは以下の github にも保存しています．

https://github.com/KazutoMakino/PythonCourse/blob/main/014_LASSO-Ridge-ElasticNet/014_LASSO-Ridge-ElasticNet.ipynb

github.com

理論と数式

LASSO

LASSO (Least Absolute Shrinkage and Selection Operator，ラッソ回帰）とは，線形回帰モデルの学習に正則化項として L1 ノルムを用いた回帰モデルで，線形回帰モデルよりも過学習を抑制することができます．
．．．と，ここで色々な用語が出てきたので，順を追って説明していきます．

過学習 (overfitting) とは，モデルが学習データにフィットしすぎて，学習に用いていない未知のデータには上手く汎化されないという問題です．これの原因の一つとして，パラメータが大きくなりすぎた結果，データに対してモデルが複雑になりすぎることが挙げられます．
正則化 (reglarization) は，損失関数に正則化項と呼ばれるペナルティ項を加えた関数を最小化することで，モデルが学習データに対する過度なフィッティングを抑制しつつ，より単純になる（≒パラメータが少なくなる）ように促す効果を持ちます．
正則化項に L1 ノルムを用いる場合（L1 正則化）は LASSO，L2 ノルムを用いる場合（L2 正則化）は Ridge 回帰（リッジ回帰）と呼ばれます．
“L” は \(L^p\) 空間を提唱したルベーグ積分でおなじみの数学者アンリ・レオン・ルベーグ（Henri Leon Lebesgue）に由来しています．

ノルムはベクトルの大きさを表し，p を自然数としたとき (\(p \in \mathbb{N})\)，ベクトル \(\boldsymbol{x} = (x_1, x_2, \cdots, x_n) \) の Lp ノルム \(\| \boldsymbol{x} \|_p\) は次で定義されます．

$$
\|\boldsymbol{x}\|_p
:= \left( \sum_{i=1}^{n} |x_i|^p \right)^{\frac{1}{p}}
= \sqrt[p]{|x_1|^p +|x_2|^p + \cdots + |x_n|^p}
$$

例えば p = 2 のとき，つまり L2 ノルムは，

$$
\|\boldsymbol{x}\|_2 := \sqrt{|x_1|^2 +|x_2|^2 + \cdots + |x_n|^2}
$$

で，これはユークリッドノルムと言われ，ご存知のとおりユークリッド空間上におけるベクトルの大きさを表しています．
n = 2 のとき，つまり２次元空間上の L1 ノルム，L2 ノルムを図示すると下図のようになります．

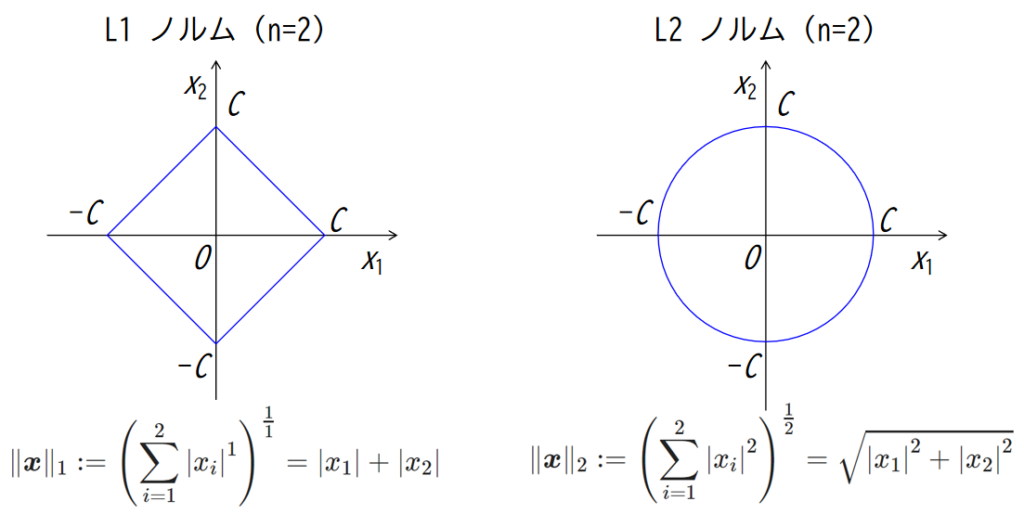
L1 ノルムは正方形を45°傾けた形，L2 ノルムなんかはそのまま円の方程式ですね．

さて，LASSO は線形回帰モデルの学習するときの最小二乗法に正則化項として L1 ノルムを用いた回帰モデルという説明をしていましたが，数式で表すと次式です．

$$
E_{LASSO}(\boldsymbol{w}) = \sum_{i=1}^{n}{\left( y_i – \hat{y_i} \right)^2} + \alpha \| \boldsymbol{w} \|_1
$$

ここで，\(E_{LASSO}(\boldsymbol{w})\) は最小化させたい誤差関数，\(y\) は正解の値，\(\hat{y}\) は予測値（説明変数 \(x_i\) と回帰係数＝重み \(w_i\) の線形結合，つまり， \(\hat{y_i} = w_i x_i\)），\(\alpha\) は正則化の強さを調整できるハイパーパラメータで，右辺第１項が最小二乗コスト関数，右辺第２項が正則化項で L1 正則化を表します．
正則化項は，「モデルのパラメータの重みに追加の制約を与える」という文脈で「ペナルティ項」とも呼ばれます．

Ridge 回帰

LASSO は L1 正則化でしたが Ridge 回帰は L2 正則化を用います．
違いはそれだけです．

$$
E_{Ridge}(\boldsymbol{w}) = \sum_{i=1}^{n}{\left( y_i – \hat{y_i} \right)^2} + \alpha \| \boldsymbol{w} \|_2
$$

Elastic Net

LASSO との違いは，右辺第２項の正則化に L1 ノルム，第３項の正則化に L2 ノルムを用いているところで，LASSO と Ridge 回帰を係数 \(r \ (0 \le r \le 1)\) によってバランスさせています．
この \(r\) もハイパーパラメータになります．

$$
E_{ElasticNet}(\boldsymbol{w}) = \sum_{i=1}^{n}{\left( y_i – \hat{y_i} \right)^2} + r \alpha \| \boldsymbol{w} \|_1 + (1 – r) \alpha \| \boldsymbol{w} \|_2
$$

コード実装と可視化例

LASSO / Ridge 回帰 / Elastic Net それぞれの引数は以下のとおりです．
（Ridge のみ scikit-learn に分類問題でも使える RidgeClassifier がライブラリに同梱されています）

LASSO (https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html) :

sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')  
- alpha=1.0： (float) 正則化の強さを調整するハイパーパラメータで，alpha は [0, inf) の値である必要があります．
- fit_intercept=True： (bool) 切片を計算する場合は True，切片を 0 として計算する場合は False にします．
- max_iter=1000： (int) 計算の最大反復回数を指定します．
- tol=0.0001： (float) 最適化の許容範囲を指定します．この値以下になるか max_iter に到達するまで計算します．
- positive=False： (bool) True にすると係数が強制的に正になります．
- random_state=None： (int) 乱数シードを設定します．
- selection='cyclic'： (str) "cyclic" の場合は説明変数を順番に用い，"random" の場合は反復計算のたびにランダム係数が更新されます．"random" の場合は，特に tol=0.0001 よりも高い場合に収束が高速化されやすくなるそうです．

他の引数については気にしなくて OK です．

Ridge / RidgeClassifier (https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html, https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RidgeClassifier.html) :

sklearn.linear_model.Ridge(alpha=1.0, *, fit_intercept=True, copy_X=True, max_iter=None, tol=0.0001, solver='auto', positive=False, random_state=None)　　
- alpha=1.0： (float) 正則化の強さを調整するハイパーパラメータで，alpha は [0, inf) の値である必要があります．
- fit_intercept=True： (bool) 切片を計算する場合は True，切片を 0 として計算する場合は False にします．
- max_iter=None： (int) 計算の最大反復回数を指定します．None の場合はパラメータ "solver" の設定によって変わり，solver が "sparse_cg", "lsqr" のとき scipy.sparse.linalg の設定値に依存し, "sag" では 1000, "lbfgs" では 15000 になります．
- tol=0.0001： (float) 最適化の許容範囲を指定します．この値以下になるか max_iter に到達するまで計算します．
- solver='auto'： (str) 以下のソルバーが選択できます．
    - "auto"： データによって自動で決定します．
    - "svd"： Singular Value Decomposition
    - "cholesky"： scipy.linalg.solve
    - "sparse_cg"： scipy.sparse.linalg.cg
    - "lsqr"： scipy.sparse.linalg.lsqr
    - "sag"： Stochastic Average Gradient descent
    - "saga"： "sag" の改良版
    - "lbfgs"： scipy.optimize.minimize
- positive=False： (bool) True にすると係数が強制的に正になります．
- random_state=None： (int) 乱数シードを設定します．

他の引数については気にしなくて OK です．

sklearn.linear_model.RidgeClassifier(alpha=1.0, *, fit_intercept=True, copy_X=True, max_iter=None, tol=0.0001, class_weight=None, solver='auto', positive=False, random_state=None)
- alpha=1.0： (float) 正則化の強さを調整するハイパーパラメータで，alpha は [0, inf) の値である必要があります．
- fit_intercept=True： (bool) 切片を計算する場合は True，切片を 0 として計算する場合は False にします．
- max_iter=None： (int) 計算の最大反復回数を指定します．None の場合はパラメータ "solver" の設定によって変わり，solver が "sparse_cg", "lsqr" のとき scipy.sparse.linalg の設定値に依存し, "sag" では 1000, "lbfgs" では 15000 になります．
- tol=0.0001： (float) 最適化の許容範囲を指定します．この値以下になるか max_iter に到達するまで計算します．
- class_weight=None： (dict or "balanced") 辞書型を使って {class_label: weight} といったフォーマットで各クラスの重みを定義できます．デフォルトの None の場合，重みは全てのクラスに対して 1 が適用されます．"balanced" の場合は y の値を使用して，n_samples / (n_classes * np.bincount(y)) のように入力データのクラス頻度に反比例するように重みを自動的に調整します．
- solver='auto'： (str) 以下のソルバーが選択できます．
    - "auto"： データによって自動で決定します．
    - "svd"： Singular Value Decomposition
    - "cholesky"： scipy.linalg.solve
    - "sparse_cg"： scipy.sparse.linalg.cg
    - "lsqr"： scipy.sparse.linalg.lsqr
    - "sag"： Stochastic Average Gradient descent
    - "saga"： "sag" の改良版
    - "lbfgs"： scipy.optimize.minimize
- positive=False： (bool) True にすると係数が強制的に正になります．
- random_state=None： (int) 乱数シードを設定します．

他の引数については気にしなくて OK です．

Elastic Net (https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.ElasticNet.html) :

sklearn.linear_model.ElasticNet(alpha=1.0, *, l1_ratio=0.5, fit_intercept=True, precompute=False, max_iter=1000, copy_X=True, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')
- alpha=1.0： (float) L1 正則化の強さを調整するハイパーパラメータで，alpha は [0, inf) の値である必要があります．
- l1_ratio=0.5： (float) L1 正則化と L2 正則化の割合を調整するハイパーパラメータで，l1_ratio は [0, 1] の値である必要があります．l1_ratio=1.0 のときは L1 正則化のみ行い L2 正則化は適用されません．
- fit_intercept=True： (bool) 切片を計算する場合は True，切片を 0 として計算する場合は False にします．
- max_iter=1000： (int) 計算の最大反復回数を指定します．
- tol=0.0001： (float) 最適化の許容範囲を指定します．この値以下になるか max_iter に到達するまで計算します．
- positive=False： (bool) True にすると係数が強制的に正になります．
- random_state=None： (int) 乱数シードを設定します．
- selection='cyclic'： (str) "cyclic" の場合は説明変数を順番に用い，"random" の場合は反復計算のたびにランダム係数が更新されます．"random" の場合は，特に tol=0.0001 よりも高い場合に収束が高速化されやすくなるそうです．

他の引数については気にしなくて OK です．

scikit-learn 自体の使い方は「モデル定義（インスタンス生成）」→「fit」→「predict」とするだけで共通なので，ここでは LASSO のみについてライブラリの使用例を示します．
今回使うライブラリをインポートします．

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

from sklearn.linear_model import Lasso

例として，簡単なデータを作り，それに対して LASSO によって回帰を計算してみましょう．
まずはデータを準備します．

# 離散点 x, y を定義
x = np.arange(0, 5).reshape(-1, 1)
y = np.array([5, 2, 4, 3, 1])

matplotlib にて可視化してみましょう．
（matplotlib の使い方はこちら：https://slash-z.com/matplotlib-first-step/）

fig = plt.figure(facecolor="white")
ax = plt.axes()
ax.scatter(x, y)
ax.set_xlim(-1, 6)
ax.set_ylim(-1, 6)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_aspect(aspect="equal")
fig.tight_layout()
plt.show()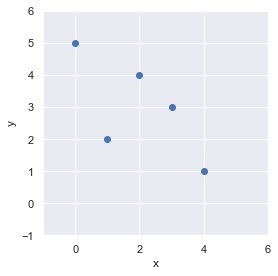

それでは，説明変数を x，目的変数を y としてモデル定義→学習→予測の３ステップで，このデータに対する回帰を計算してみましょう．

# モデル定義
model = Lasso(alpha=1.0, random_state=0)
# 学習
model.fit(x, y)
# 予測
y_pred = model.predict(x)
print(y_pred)
# array([3.4, 3.2, 3. , 2.8, 2.6])

元データと予測値を可視化してみましょう．

fig = plt.figure(facecolor="white")
ax = plt.axes()
ax.axvline(x=0, color="gray", linestyle="--")
ax.axhline(y=0, color="gray", linestyle="--")
ax.plot(x, y_pred, color="red", marker="o", markerfacecolor="white")
ax.scatter(x, y, color="black", marker="x")
ax.set_xlim(-1, 6)
ax.set_ylim(-1, 6)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_aspect(aspect="equal")
fig.tight_layout()
plt.show()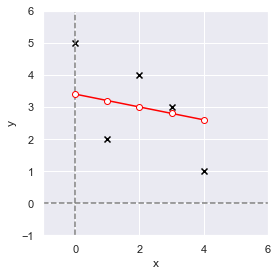

次は，データ点が多い場合も見てましょう．
まずは，以下で 0 から 100 まで 0.1 刻み幅の数列の x に対し y=x に ±5 をランダムに与えたデータとして定義します（numpy の使い方：https://slash-z.com/python-numpy-firststep/）．
線形回帰式は，傾きが１，切片が０になるイメージです．

# 指定乱数シードによるランダムジェネレータを設定
rng = np.random.RandomState(seed=0)

# x, y を定義
x = np.arange(start=0, stop=100 + 0.1, step=0.1)
y = x + rng.uniform(low=-5, high=5, size=len(x))
x = x.reshape(-1, 1)

print(x.shape, y.shape)
# (1010, 1) (1010,)

学習用データとモデルの検証用データを分けるため，scikit-learn の train_test_split を用います．
種々のデータ分割の手法については，こちらの記事（https://slash-z.com/data-split-of-cross-validation/）をご参照ください．

from sklearn.model_selection import train_test_split

# 学習用と評価用のデータをシャッフルせずに 6 : 4 に分ける
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4, shuffle=False)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
# (600, 1) (401, 1) (600,) (401,)

データを可視化すると，次のようになっています．

fig = plt.figure(facecolor="white")
ax = plt.axes()
ax.scatter(x_train, y_train, marker=".", label="train")
ax.scatter(x_test, y_test, marker=".", label="test")
ax.set_aspect(aspect="equal")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.legend(loc="upper left")
fig.tight_layout()
plt.show()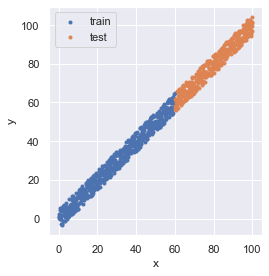

それでは，これについて LASSO で回帰を計算してみましょう．

model = Lasso(alpha=1.0, random_state=0)
model.fit(X=x_train, y=y_train)
y_pred = model.predict(x)

ここで，推論は学習用／検証用データ全体に対して計算していますが，検証用のみ精度確認したい場合は，適宜 x の代わりに x_test としてください．
推論結果を可視化しましょう（回帰で求めた予測値をライム色の線としています）．

fig = plt.figure(facecolor="white")
ax = plt.axes()
ax.scatter(x_train, y_train, marker=".", label="train")
ax.scatter(x_test, y_test, marker=".", label="test")
ax.plot(x, y_pred, color="lime")
ax.set_aspect(aspect="equal")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.legend(loc="upper left")
fig.tight_layout()
plt.show()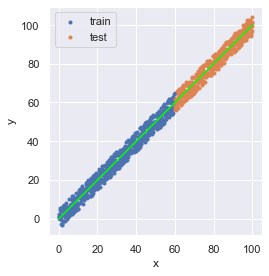

想像通りの結果になったと思います．

演習問題

Q1. ワインデータセットについて，以下を参照して，目的変数であるワインの等級を LASSO によって求めてください．

• データ分割は train_test_split にて行い，学習用データは全データの 90 %，データのシャッフルは True としてください（結果に再現性を持たせたい場合は，引数 random_state に任意の数を設定してください）
• データは，以下のコードにて読み込むことができます（データの説明はこちら：https://slash-z.com/matplotlib-first-step/）

from sklearn.datasets import load_wine

df_x, df_y = load_wine(return_X_y=True, as_frame=True)

Q2. 上記で学習したモデルを用いて，df_x 全データについて推論を計算し，分類精度を計算しましょう．
分類問題に無理やり回帰を用いていることから，推論結果は float となるため，例えば推論結果に .astype(np.uint8) としてカテゴリ変数に変換してください．
for / if 文を用いても精度は計算できますが，scikit-learn を用いて分類問題における認識精度を確認するには，以下のようにして算出が可能です．
ここで，y_true は正解ラベルの df_y，y_pred には df_x に対するモデルの推論結果を代入してください．

from sklearn.metrics import accuracy_score

print(accuracy_score(y_true, y_pred))

Q3. 上記の結果について，他の linear_model である　LinearRegression, Lasso, RidgeClassifier, ElasticNet で認識精度を比較してみましょう．注意として RidgeClassifier のみクラス分類できるモデルになっているため，Q2 で対応した .astype(np.uint8) とする処理は不要です．

Q4. カリフォルニア住宅価格データセットについて，LASSO を用いて以下の手順で住宅価格を予測してみましょう．

• 次のコードでデータ読み込み，学習用／検証用にデータを分割します．

from sklearn.datasets import fetch_california_housing

df_x, df_y = fetch_california_housing(return_X_y=True, as_frame=True)
x_train, x_test, y_train, y_test = train_test_split(
    df_x, df_y, test_size=0.25, shuffle=True, random_state=0,
)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)

• 学習用データ (x_train, y_train) のみを学習し，検証用データ x_test について住宅価格を予測しましょう．
• 上記で予測した住宅価格について，正解の値との絶対平均誤差を算出してみましょう．

以下のコードにて絶対平均誤差が算出できます．
ここで，y_true は正解データの y_test，y_pred には x_test に対するモデルの推論結果を代入してください．

from sklearn.metrics import mean_absolute_error

print(mean_absolute_error(y_true, y_pred))

Q5. 上記の結果について，他の linear_model である　LinearRegression, Lasso, Ridge, ElasticNet で認識精度を比較してみましょう．今回は回帰問題で誤差を算出しているので，誤差が小さいほど良い精度で予測しています．

演習問題の解答

import numpy as np
from sklearn.datasets import load_wine
from sklearn.metrics import accuracy_score
from sklearn import linear_model
from sklearn.model_selection import train_test_split

# データ読み込み
df_x, df_y = load_wine(return_X_y=True, as_frame=True)

# データ分割
x_train, x_test, y_train, y_test = train_test_split(
    df_x, df_y, test_size=0.1, shuffle=True, random_state=0,
)

# 学習／推論
model = linear_model.Lasso()
model.fit(x_train, y_train)
pred = model.predict(df_x)

# float -> int
pred_cate = pred.astype(np.uint8)

# 分類精度算出
print(accuracy_score(y_true=df_y, y_pred=pred_cate))
# 0.6741573033707865

for model in (
    linear_model.LinearRegression(),
    linear_model.Lasso(),
    linear_model.RidgeClassifier(),
    linear_model.ElasticNet(),
):
    # 学習／推論
    model.fit(x_train, y_train)
    pred = model.predict(df_x)
    # float -> int
    if isinstance(model, linear_model.RidgeClassifier):
        pred_cate = pred
    else:
        pred_cate = pred.astype(np.uint8)

    # 分類精度算出
    print(model, accuracy_score(y_true=df_y, y_pred=pred_cate))
# LinearRegression() 0.6179775280898876
# Lasso() 0.6741573033707865
# RidgeClassifier() 1.0
# ElasticNet() 0.6460674157303371

from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_absolute_error

# データ読み込み／分割
df_x, df_y = fetch_california_housing(return_X_y=True, as_frame=True)
x_train, x_test, y_train, y_test = train_test_split(
    df_x, df_y, test_size=0.25, shuffle=True, random_state=0,
)

# 学習／推論
model = linear_model.Lasso()
model.fit(x_train, y_train)
pred = model.predict(x_test)

print(mean_absolute_error(y_true=y_test, y_pred=pred))
# 0.7687270988960119

for model in (
    linear_model.LinearRegression(),
    linear_model.Lasso(),
    linear_model.Ridge(),
    linear_model.ElasticNet(),
):
    # 学習／推論
    model.fit(x_train, y_train)
    pred = model.predict(x_test)

    print(model, mean_absolute_error(y_true=y_test, y_pred=pred))
# LinearRegression() 0.5368950735045219
# Lasso() 0.7687270988960119
# Ridge() 0.5369060034129463
# ElasticNet() 0.6805978110367683

機械学習の勉強でおすすめの本

“Python機械学習プログラミング 達人データサイエンティストによる理論と実践” は 500 ページ超もあり，理論や実装についてしっかり書かれているため，体系的・網羅的に学習できます．
しかしながら超大作であるため，初学者が全部を一から読み進めて行くという使い方だと，よほどの根気がなければ挫折すると思います．
また，数式もちゃんと書かれているのですが，基礎的な解析学や線形代数学などの知識があること前提に書かれていますので，大学のときの教科書や参考書，web 記事なども参考にする必要があります．
従いまして，見たいところだけを随時見たり，ある程度身についてきてからハンドブック的に用いることを推奨します．
筆者は，こちらの第２版を購入しており，今もハンドブック的な役割で使っています．

数学の知識について，個人的には，演習問題もついててお得な，以下の書籍をハンドブック的に参考にすることが多いです．
深く内容を見返したい場合は，大学のときの教科書や参考書を見ています．