【自前AI講座】ディープラーニング基礎と実装

dl プログラミング
2023.02.13



ディープラーニング (Deep Learning; DL，深層学習) は，ニューラルネットワークの層を深くしたディープニューラルネットワーク (Deep Neural Network; DNN) を用いて学習する手法です．
（ニューラルネットワークについては，こちらの記事 (https://slash-z.com/neural-network/) にまとめました．）
何かを認識したり，予測したりするシステムを構築するときに，昔は，問題ごとに専用のアルゴリズムを開発したり，特徴量を計算させた後，統計処理などによって制御信号として与えていました．
このため，その問題の現象や中身を理解している専門家でないと，こういったシステム構築は困難でした．
ディープラーニングの登場により，良質で大量のデータが用意できれば予測モデルを学習することができるため，専門家の知見が必要であった特徴量抽出などの専門領域の理解は（ほとんど）不要になりました．
今回は，このディープラーニングについて，フレームワークの一つである TensorFlow による実装とともに紹介していきます．
また，ニューラルネットワークの記事で紹介しきれなかった手法についても触れていきます．

コードは github 上にも置いています．

https://github.com/KazutoMakino/PythonCourse/blob/main/018_DeepLearning/018_DeepLearning.ipynb
github.com

ディープラーニングの簡単な実装

ニューラルネットワークでは，層を深くしたりニューロンを増やすことで，表現力が強化できました．
ディープラーニングはニューラルネットワークを「層を重ねて深くしただけ」と言われればそれまでです．
どこからディープかと言われると人によってまちまちですが，こちらの書籍では隠れ層が４つ以上だと一般に呼ばれるとのことです．
なので定義をあえて書くなら，ディープラーニング = ４層以上のニューラルネットワークということになります．
実装を交えて紹介していくため，まずは，ディープラーニングのフレームワークの一つである TensorFlow (テンサーフロー／テンソルフロー，https://www.tensorflow.org/api_docs/python/tf) を用いた例を示します．
（他のフレームワークとしては，pytorch, jax/flax などがあるのですが，比較については後日，他の記事にて寄稿しようと思います．）
ここで条件として，

  • ニューラルネットワーク構造・・・・簡単のため隠れ層が4層で各ニューロンの数を 32 個とした全結合層のみ
  • 対照データ・・・・フリーの手書き数字データセットである mnist （エムニスト，matplotlib の回で示した手書き数字データセット (https://i0.wp.com/slash-z.com/wp-content/uploads/2022/07/answer_02.png?w=856&ssl=1) の高画質版で，8bit グレイスケール 28×28 [px] 画像が学習用：50,000 個，検証用：10,000 個あるデータセット）
  • 活性化関数・・・・隠れ層： ReLU，出力層： Softmax
  • 最適化関数・・・・確率的勾配降下法 (SGD) で学習率は 0.01
  • 損失関数・・・・交差エントロピー誤差
  • ミニバッチサイズ・・・・32
  • epoch 数（ミニバッチを全て学習して１）・・・・とりあえず 5
  • （個人的な好みで Functional API／標準のトレーニングループ・・・・y = f(x) を並べていくだけのような書き方です．詳細はフレームワーク紹介の記事で記載予定です．）
import numpy as np
import tensorflow as tf
from keras import layers, optimizers, metrics, losses, Model, callbacks

# データセット準備
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
print(x_train.shape, y_train.shape, x_test.shape, y_test.shape)
print(x_train.dtype, y_train.dtype, x_test.dtype, y_test.dtype)

# 画素値を 0～255 から 0～1 に正規化
x_train = x_train.astype(np.float32) / 255.0
x_test = x_test.astype(np.float32) / 255.0

# クラス数を算出
classes = len(set(y_train))

# モデル定義
inputs = layers.Input(shape=x_train.shape[1:])
x = inputs
x = layers.Flatten()(x)
x = layers.Dense(units=32)(x)
x = layers.ReLU()(x)
x = layers.Dense(units=32)(x)
x = layers.ReLU()(x)
x = layers.Dense(units=32)(x)
x = layers.ReLU()(x)
x = layers.Dense(units=32)(x)
x = layers.ReLU()(x)
x = layers.Dense(units=classes)(x)
x = layers.Softmax()(x)
outputs = x
model = Model(inputs=inputs, outputs=outputs)
# 最適化関数，損失関数，評価関数の定義
model.compile(
    optimizer=optimizers.SGD(learning_rate=0.01),
    loss=losses.SparseCategoricalCrossentropy(),
    metrics=[metrics.SparseCategoricalAccuracy()],
)

# 学習
model.fit(x=x_train, y=y_train, batch_size=32, epochs=5)

# (60000, 28, 28) (60000,) (10000, 28, 28) (10000,)
# uint8 uint8 uint8 uint8
# Epoch 1/5
# 1875/1875 [==============================] - 4s 2ms/step - loss: 1.1316 - sparse_categorical_accuracy: 0.6453
# Epoch 2/5
# 1875/1875 [==============================] - 4s 2ms/step - loss: 0.3337 - sparse_categorical_accuracy: 0.9029
# Epoch 3/5
# 1875/1875 [==============================] - 3s 2ms/step - loss: 0.2527 - sparse_categorical_accuracy: 0.9256
# Epoch 4/5
# 1875/1875 [==============================] - 3s 2ms/step - loss: 0.2087 - sparse_categorical_accuracy: 0.9389
# Epoch 5/5
# 1875/1875 [==============================] - 3s 2ms/step - loss: 0.1801 - sparse_categorical_accuracy: 0.9474
# <keras.callbacks.History at 0x25a88249cf0>

今回はそれぞれの API の説明をすると膨大な量になるので割愛して，上記コードについて説明します．

  • import について：
    • tensorflow は tf とするのが一般的なので，as tf としています．
    • keras というライブラリも読んでいますが，これは TensorFlow がバージョン２に上がる際に統合された元々は別だったディープラーニングのフレームワークで，tf.keras で呼ぶことができるのですが，この場合だと VSCode でコード補完が効かないので，keras から直接インポートしています．
  • tf.keras.datasets.mnist.load_data() で学習用／検証データがタプルで返ってくるので，コードの通り読み込んでいます (https://www.tensorflow.org/api_docs/python/tf/keras/datasets/mnist/load_data)．
  • 8bit 深度グレイスケール画像なので，画素値を 0～255 から 0～1 に正規化
  • 出力層の数であるクラス数をラベルデータのユニークな個数から算出
  • ニューラルネットワーク構造の定義：
    • layers.Input(shape=x_train.shape[1:])・・・・入力層を定義しています．x_train[0] はデータ数なので除外しています．
    • x = layers.Flatten()(x)・・・・画像一枚の形状が (28, 28) なので，これを全結合層に入れるために (28*28, ) と変形させる層です．この層は学習パラメータはありません．
    • x = layers.Dense(units=32)(x)・・・・全結合層を定義します．units でニューロンの数が定義できます．
    • x = layers.ReLU()(x)・・・・ReLU による活性化関数の層です．
    • x = layers.Softmax()(x)・・・・Softmax による活性化関数の層です．
    • model = Model(inputs=inputs, outputs=outputs)・・・・入力層と出力層を与えてニューラルネットワークモデルを定義します．
    • model.compile(optimizer=optimizers.SGD(learning_rate=0.01), loss=losses.SparseCategoricalCrossentropy(), metrics=[metrics.SparseCategoricalAccuracy()])・・・・最適化関数 (optimizer)，損失関数 (loss)，評価関数 (metrics) を定義します．SparseCategoricalCrossentropy は交差エントロピー誤差で，一般的には出力は one-hot ベクトル（0 と 1 のみからなる正解データを 1，その他を 0 としたクラス数次元のベクトル）にする必要があるのですが，これを用いることで one-hot ベクトルへの変換が不要です．
  • model.fit(x=x_train, y=y_train, batch_size=32, epochs=5)・・・・scikit-learn のように，model.fit で学習ができます．

学習データに対する認識精度は 95 % 程度と高い認識精度となりましたが，正直 mnist は簡単なので，これよりも簡単なニューラルネットワークでも十分高い精度がでます．
しかしながら，他の一般的な問題において，ただ層を深くしただけでは性能向上に限界があったため，解決するための色々なアイディアが生まれました．
これについて以降の章にて取り扱います．
また，実用上良く使う処理についても合わせて記載していきます．

勾配消失問題とその対策

ニューラルネットワークの層を重ねることで問題となるのが，学習する際の誤差逆伝播のときに計算される誤差の勾配は層が多ければ多いほど小さくなってしまうという「勾配消失問題 (vanishing gradient problem)」です．

活性化関数

勾配消失問題の緩和策の一つとしては活性化関数の変更が挙げられます．
なぜならば，層が多ければ多いほど活性化関数の微分もかけ合わせられるからです．
これは，実は隠れ層の活性化関数をシグモイド関数から ReLU 関数に変更することで緩和できます．
ReLU 関数についてはニューラルネットワークの回にて紹介していますので，こちらをご覧ください．

【自前AI講座】ニューラルネットワーク
Chat GPT / Stable Diffusion / 自動運転技術を筆頭に，今や AI といえば Deep Learning の時代といっても過言ではないでしょう（もちろん，スパースモデリングなども今後ブームとなる可能性もあります）．...
slash-z.com
2023.02.08

単純パーセプトロンの例としますが，ニューラルネットワークの回で，

  • 活性化関数：シグモイド関数　\(h(a) = 1 \ / \ (1 + \exp(-a))\)
  • 損失関数：二乗平均誤差　\(E = (y – t)^2 \ / \ 2\)

とした場合，（確率的）勾配降下法による重み更新の式は，

$$
w_i \leftarrow w_i – \eta \ x_i \ (t – y) \ (1-y) \ y
$$

でした．
ここで，\(w_i\) は重み，\(\eta\) は学習率，\(x_i\) は入力，\(t\) は正解データ，\(y\) は出力です．
この式の \((1 – y) \ y\) は，活性化関数であるシグモイド関数の微分の

$$
\frac{\partial h(a)}{\partial a} = (1-y) \ y
$$

でした．
そこで，活性化関数を ReLU 関数

$$
h(a) =
\begin{cases}
a & (a \gt 0) \\
0 & (a \le 0)
\end{cases}
$$

とすると，この微分は，

$$
\frac{\partial h(a)}{\partial a} =
\begin{cases}
1 & (a \gt 0) \\
0 & (a \le 0)
\end{cases}
$$

になるため，これを重み更新の式に用いると，

$$
w_i \leftarrow w_i
\begin{cases}
– \eta \ x_i \ (t – y) & (a \gt 0) \\
0 & (a \le 0)
\end{cases}
$$

となり，出力 \(y\) による影響が大きく緩和されることが分かります．
（多層になった場合はもう少し複雑です．）
他にも色々な活性化関数があるのですが，記事一つ掛けてしまうので，今回は割愛します．
コード実装については，既に最初の例で示しているので省略します．

重みの初期値

勾配消失の緩和策としては，他には各層の重みの初期値を適切に与えることです．
何も学習していないネットワークにおいて，各層の重みの初期値は一定値もしくはランダムで与えるしか手段がありませんが，初期値として与える乱数の分布も重要になってきます．
乱数というと，一様乱数やガウス分布の正規乱数などが思い浮かびますが，ディープラーニングにおける重みの初期値としては，これらは不適です．
実際には，作用する活性化関数の形状によって，点対称な活性化関数ならば Xavier（読み方は「ゼイビア」「ザビエル」？）の初期値（「Glorot の初期値」とも，考案者が Xavier Glorot さんでどちらでも呼ばれる），点対称でないなら He（読み方は「フー」？）の初期値を用いるのが一般的とされています．
前の層のニューロンの数を \(n\) とすると，正規乱数から \(n\) 個取ってきた配列に対して，Xavier の初期値 (http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf) では \(\sqrt{1 / n}\) かけた値，He の初期値 (https://arxiv.org/abs/1502.01852) では \(\sqrt{2 / n}\) かけた値を用います．
\(n = 256\) として３つの分布のカーネル密度推定（ヒストグラムだとボコボコだったので）をグラフ化したのが次です．

neuron_num = 256
rng = np.random.default_rng(seed=0)
rng_normal = rng.normal(size=neuron_num)
rng_xavier = rng_normal * math.sqrt(1 / neuron_num)
rng_he = rng_normal * math.sqrt(2 / neuron_num)

plt.figure(figsize=(10, 3), facecolor="white")
sns.kdeplot(rng_normal, color="black", label="Normal")
sns.kdeplot(rng_xavier, color="red", label="Xavier")
sns.kdeplot(rng_he, color="blue", label="He")
plt.legend(loc="upper right")
plt.tight_layout()
plt.show()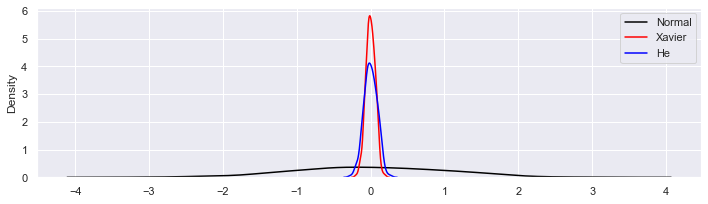
dl-03

分布の裾野の広がり方としては，正規乱数 >> He の初期値 > Xavier の初期値 になりました．

TensorFlow では “kernel_initializer” という引数がある層について定義が可能で，

x = layers.Dense(units=units, kernel_initializer="he_normal")(x)

といった具合に書きます．
初期値は “glorot_uniform” で Xavier の初期値です．
He の初期値を用いたいときは “he_normal” を指定します．

バッチ正規化

勾配消失の緩和策としてはもう一つ，バッチ正規化 (batch normalization) が挙げられます．
バッチ正規化は，ミニバッチごとにデータの分布が平均０，分散１になるように正規化を行います．
\(m\) 個の入力データが入ったミニバッチ \(B = {x_1, \ x_2, \ \cdots, \ x_m}\) に対し，バッチ正規化後の入力 \(\hat{x_i}\) は，入力 \(x_i\) の平均 \(\mu_B\) と分散 \(\sigma_B^2\) を用いて，

$$
\hat{x_i} \leftarrow \frac{x_i – \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}
$$

として与えられます．
ここで，\(\epsilon\) は式が０で除算されないための十分小さな値で，例えば \(10^{-7}\) などが代入されます．
また，バッチ正規化ではこの正規化されたデータに対して，

$$
y_i \leftarrow \gamma \hat{x_i} + \beta
$$

というように，スケール \(\gamma\) とシフト量 \(\beta\) を学習していって，データの分布の偏りがないように調整されていきます（\(\gamma\) は 1，\(\beta\) は 0 をそれぞれ初期値とします）．

バッチ正規化の良いところとしては，

  • 学習を速く進行させることができる
  • 初期値に大きく依存しない
  • 過学習を抑制する作用がある

が挙げられます．

バッチ正規化をニューラルネットワークのどの部分に挿入するかは色々議論はありますが，活性化関数の前後どちらかに挿入するのが一般的です．

あとは，畳み込みニューラルネットワークや回帰型ニューラルネットワークに用いられる手法もあるのですが，それぞれの記事で紹介することにします．

TensorFlow による実装としては，

x = layers.BatchNormalization()(x)

とすることで，バッチ正規化を追加することが可能です．

最適化関数

Adam (https://arxiv.org/abs/1412.6980v8 , Adaptive moment) は SGD の数段階進化した最適化アルゴリズムで，他の最適化アルゴリズムであるモーメンタムと RMSprop を混合させたようなアルゴリズムです．
特徴としては，変数空間の勾配が小さい方向に対しても更新されやすいことが挙げられます．
数式で表すと SGD より複雑ですが，最適化したい変数 \(\theta\) について 時間ステップが \(t\) ステップ目の値 \(\theta_t\) は \(t-1\) ステップの値 \(\theta_{t-1}\) を用いて次式のように書くことができます．

$$
\theta_t \leftarrow \theta_{t-1} – \eta \frac{\hat{m_t}}{\sqrt{\hat{\nu_t}} + \epsilon}
$$

ここで，

$$
\hat{m_t} \leftarrow \frac{m_t}{1 – \beta_1^{(t)}} \\
\hat{\nu_t} \leftarrow \frac{\nu_t}{1 – \beta_2^{(t)}} \\
m_t \leftarrow \beta_1 m_{t-1} + (1 – \beta_1) g_t \\
\nu_t \leftarrow \beta_2 \nu_{t-1} + (1 – \beta_2) g_t^2
$$

であり，\(\eta\) は学習率，\(\epsilon\) は０で除算されないための小さい値，\(m\) はモーメンタムに用いられる勾配の１乗和，\(\nu\) は RMSprop に用いられる勾配の２乗和，\(\beta_1, \ \beta_2\) はモーメンタムの指数関数的減衰 (exponential decay) に用いられるパラメータ (\(0 \le \beta \lt 1\))，\(g_t\) は時刻 \(t\) の勾配を表します．

他にも色々あるのですが，基本的には Adam を押さえておけば十分です．
必要に応じて情報収集していけば良いと思います．

TensorFlow では最適化関数を設定するところで，

model.compile(optimizer=optimizers.Adam())

とすることで指定できます．

データ分割

構築した AI モデルにおいて実運用を考えると，汎化性能（学習に用いたデータのみならず，学習に用いていない未知のデータに対する予測性能）の向上は重要です．
クラス分類のような教師あり学習では，ラベルデータの不均衡（データの偏り）があったり，学習データが少ないと，上手く学習がいかなかったり，学習データに依存したバイアスがかかって汎化性能が落ちることがあります．
そこで重要になってくるのが，学習データの分割です．
汎化性能を上げるためには，一般的には，学習データの他に学習に用いない検証用データを別で保持しておいて，毎 epoch の学習結果に対する認識精度を評価し，その推移によって汎化性能が検証できます（ただし，検証用データが未知のデータに対しても不均衡でないときに限ります）．

今回の例では，学習用データが _train，検証用データが _test という風に既にデータ分割されているので，TensorFlow で epoch 毎に評価データの認識精度を計算させるためには，学習させる model.fit のところで validation_data という引数を使って，

model.fit(
    x=x_train,
    y=y_train,
    validation_data=(x_test, y_test),
)

とすることで実装が可能です．

なお，データ分割の手法や実装については，次の記事にまとめましたのでご参照ください．

機械学習におけるデータ分割手法まとめ
機械学習において，持っているデータ全てを学習させてしまうと，そのデータの傾向に依存したバイアスがかかり，過学習に陥ることによって，モデルにおける未知のデータに対する推論性能（汎化性能）が損なわれる恐れがあります．これの対策の一つとして，デー...
slash-z.com
2022.05.13

過学習防止

学習用／評価用データを分けて学習していくことで，epoch の増加に伴い，学習用データの損失が減少しているが評価用データに対する損失が減少していかない場合，あるいは，学習用データと評価用データの認識精度が大きく乖離している場合に，過学習 (over fitting，学習に用いたデータのみに強くバイアスがかかってしまい，汎化性能が失われた状態) に陥っている場合があります．
この過学習にならないため／過学習になったモデルを用いないためには，学習時に評価用データに対しても一緒に計算させ，それを観察すること（例えば，損失が最小となったときの epoch のモデルを用いること）で回避ができます．

まずは学習中のモデルの保存について，TensorFlow では，以下のように model.fit の引数 callbacks に callbacks.ModelCheckpoint (https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/ModelCheckpoint) をリストの要素として与えることで設定が可能です．

model.fit(
    *,
    callbacks=[
        callbacks.ModelCheckpoint(
            filepath=filepath,
            monitor="val_loss",
            verbose=0,
            save_best_only=False,
            save_weights_only=False,
            mode="auto",
            save_freq="epoch",
        ),
    ],
)

ここで，引数 filepath は保存するモデルのファイルパス（拡張子は .h5 にしておくと，単一ファイルに保存可能），monitor は保存する基準としてどの値に着目するか，verbose は保存する動作を表示するかどうかで 0 の場合は非表示／1 以上であれば表示，save_best_only は monitor で指定した値が最も良い結果となった時に保存する場合は True／毎回保存する場合は False，save_weights_only は重みのみ保存したい場合は True／モデルごと保存したい場合は False，mode は monitor がどの状態になったときに保存するかを指定でき “auto” なら自動で判断／”min” なら最小となったとき（monitor に loss など最小化したいものを指定したとき）／”max” なら最大となったとき（monitor に accuracy などを指定したとき），save_freq は保存する頻度を指定できる引数で “epoch” なら毎 epoch （save_best_only=True なら最良の結果のとき）／整数型で指定した場合はその epoch 数飛ばしごとに保存します．
モデルが性能改善されるたびに保存されるためその分の保存時間が改善される epoch 毎に追加されますが，予期せぬ自体により学習が中断される事も考えると，ModelCheckpoint を入れておくのが無難でしょう．

次に，学習が数 epoch 続けてうまくいかない（精度が改善されなかったり，損失が低減しない）場合に学習を打ち切り（早期打ち切り）させるには，TensorFlow では，以下のように model.fit の引数 callbacks に callbacks.EarlyStopping (https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/EarlyStopping) をリストの要素として与えることで設定が可能です．

model.fit(
    *,
    callbacks=[
        callbacks.EarlyStopping(
            monitor="val_loss",
            min_delta=0,
            patience=0,
            verbose=0,
            mode="auto",
            baseline=None,
            restore_best_weights=False,
        ),
    ]
)

ModelCheckpoint と引数名が同じものについては役割も同じなので説明を省略します．
min_delta は性能改善幅の最低ラインを定義，patience は何回続けて改善されないかを整数型で定義，baseline は性能の最低ラインを定義，restore_best_weights は True だと model に早期打ち切り時のモデルが変数として格納／False だと最終 epoch のモデルが変数として格納されます．

他にも使えるコールバック関数は色々あるので，こちら (https://www.tensorflow.org/api_docs/python/tf/keras/callbacks) をご覧ください．

Drop out

Drop out はニューロンをランダムに消去して学習させるといった単純な手法ですが，過学習を抑制させる効果があります．
イメージとしては，意図的にランダムで選んだ脳細胞を非活性にして，残った脳細胞でも上手くいくように学習していくことで，思考の偏りがなくなる感じでしょうか．
実装としては Drop out 層としてニューラルネットワークに組み込みます．

TensorFlow では次のように実装します．

x = layers.Dropout(rate=rate)(x)

引数 rate (0 \le rate \lt 1) でニューロンの何割を削除するかを指定します．
他の引数もあるのですが，無視して大丈夫です（引数 seed で乱数シード値を指定することができますが，次の章のように全体で一括でシード値を固定することがほとんどだと思います）．

乱数シード値の固定

乱数シード値を指定しない場合は，同じコードで計算しても毎回異なる結果が出てきてしまいます．
そのため，学習の再現性を持たせたい場合は乱数シード値を固定する必要があります．
個人的には次のような関数を定義して，学習コードの最初の方で実行するようにしています．
（参考：　https://qiita.com/kaggle_grandmaster-arai-san/items/d59b2fb7142ec7e270a5#seed_everything）

def seed_everything(seed: int = 0):
    # os
    os.environ["PYTHONHASHSEED"] = str(seed)
    # random
    random.seed(seed)
    # numpy
    np.random.seed(seed)
    # tensorflow
    tf.random.set_seed(seed)
    # for GPU : https://github.com/NVIDIA/framework-determinism
    os.environ["TF_DETERMINISTIC_OPS"] = "true"
    os.environ["TF_CUDNN_DETERMINISTIC"] = "true"


seed_everything()

もちろん，必要なライブラリは予めインポートしておきましょう．
上記の場合ですと，os, random, numpy (as np), tensorflow (as tf) です．

学習率スケジューラ

学習率が一定だと，中々局所最小値近傍や重みの傾きが平坦な領域から抜け出せなかったりします．
これの対策には，学習率を動的に変えるようなスケジューラを組むことが有効です．

スケジューラの一つの方法としては，「何 epoch 学習して改善されなかったら学習率を下げる」という方法で，TensorFlow では callbacks.ReduceLROnPlateau で以下のように指定ができます．

model.fit(
    *,
    callbacks=[
        callbacks.ReduceLROnPlateau(
            monitor="val_loss",
            factor=0.1,
            patience=10,
            verbose=0,
            mode="auto",
            min_delta=0.0001,
            cooldown=0,
            min_lr=0,
        ),
    ],
)

これまで出てきた引数については省略するとして，factor は学習率を何倍するか，cooldown は一旦これが呼ばれてから何 epoch 分は patience の条件から除外するか，min_lr は最小となる学習率を表します．

スケジューラのもう一つの方法としては，「最初の方の epoch は学習が上手く行きにくいので学習率低めで epoch の増加とともに徐々に学習率を上げていき，途中からは最小値に向かわせるように滑らかに減少させていく」という考え方のスケジューラで，徐々に学習率を上げていくのが warm up で，滑らかに減少させるのが cosine decay です．
大体は一緒に用いられます．
Tensorflow による実装としては，カスタムスケジューラを組んで，それを用いるように callbacks.LearningRateScheduler (https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/LearningRateScheduler) で指定します．

warm_up_epoch = 10
max_lr = 0.001
final_epoch = 200


def lr_scheduler(epoch: int, _: float) -> float:
    if epoch <= warm_up_epoch:
        scheduled_lr = epoch / warm_up_epoch * max_lr
    else:
        scheduled_lr = (
            (
                math.cos(
                    (epoch - warm_up_epoch) / (final_epoch - warm_up_epoch) * math.pi
                )
                + 1
            )
            * max_lr
            / 2
        )
    scheduled_lr = round(scheduled_lr, ndigits=9)
    return scheduled_lr


model.fit(
    *,
    callbacks=[
        callbacks.LearningRateScheduler(
            schedule=lr_scheduler,
            verbose=0,
        ),
    ],
)

ここで，schedule は自分で定義した学習率スケジューラの関数を指定します．
上記スケジューラの学習率を可視化すると，下図のようにサメのヒレのような形をしています．

dl-04

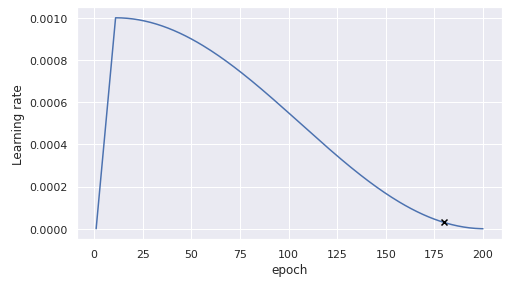
他にも様々な学習率スケジューラが考案されていますが，ここでは割愛します．

その他

ニューラルネットワーク構造の概要表示

ニューラルネットワークを定義した後，例えば model という変数で定義したなら，model.summary() で構造の概要が標準出力されます．

不要な学習済みモデルやキャッシュの削除

学習が終わった後の変数をそのままにした状態でもう一度学習すると，学習された状態から始まってしまうので，もう一度定義し直したり，削除したりすることをオススメします．
ついでにキャッシュを削除しておくと，パソコンのメモリ的にもありがたいので，個人的には以下のようにしています．

# 学習が終わって結果を取り出した後に以下を実行
try:
    del model
except Exception as err:
    pass
tf.keras.backend.clear_session()
gc.collect()

演習問題

Q. mnist を次に指定するニューラルネットワーク構造，及び，学習方法にて学習してください．

  • 隠れ層４つの全結合層で，活性化関数は ReLU （各層のニューロン数の設定は自由）
  • バッチ正規化と drop out を入れる（削除割合の設定は自由）
  • 重みの初期化については，ReLU の場合は He の初期値，Softmax の場合は Xavier の初期値を用いる
  • 学習 epoch は 30 で，学習率を上限 0.01 とした warm up が 3 の cosine decay とする
  • 評価用データの結果も毎 epoch 計算させる

演習問題の解答

Q. mnist を次に指定するニューラルネットワーク構造，及び，学習方法にて学習してください．

  • 隠れ層４つの全結合層で，活性化関数は ReLU （各層のニューロン数の設定は自由）
  • バッチ正規化と drop out を入れる（削除割合の設定は自由）
  • 重みの初期化については，ReLU の場合は He の初期値，Softmax の場合は Xavier の初期値を用いる
  • 学習 epoch は 30 で，学習率を上限 0.01 とした warm up が 3 の cosine decay とする
  • 評価用データの結果も毎 epoch 計算させる
warm_up_epoch = 3
max_lr = 0.01
final_epoch = 30


def lr_scheduler(epoch: int, _: float) -> float:
    if epoch <= warm_up_epoch:
        scheduled_lr = epoch / warm_up_epoch * max_lr
    else:
        scheduled_lr = (
            (
                math.cos(
                    (epoch - warm_up_epoch) / (final_epoch - warm_up_epoch) * math.pi
                )
                + 1
            )
            * max_lr
            / 2
        )
    scheduled_lr = round(scheduled_lr, ndigits=9)
    return scheduled_lr
tf.keras.backend.clear_session()
gc.collect()

inputs = layers.Input(shape=x_train.shape[1:])

x = inputs
x = layers.Flatten()(x)
for i in range(4):
    x = layers.Dense(units=128, kernel_initializer="he_normal")(x)
    x = layers.BatchNormalization()(x)
    x = layers.ReLU()(x)
    x = layers.Dropout(rate=0.2)(x)
x = layers.Dense(units=classes, kernel_initializer="glorot_uniform")(x)
x = layers.Softmax()(x)
outputs = x

model = Model(inputs=inputs, outputs=outputs)
model.compile(
    optimizer=optimizers.Adam(learning_rate=0.001),
    loss=losses.SparseCategoricalCrossentropy(),
    metrics=[metrics.SparseCategoricalAccuracy()],
)

model.summary()

model.fit(
    x=x_train,
    y=y_train,
    validation_data=(x_test, y_test),
    batch_size=32,
    epochs=30,
    callbacks=[
        callbacks.ModelCheckpoint(
            filepath="./model.h5",
            monitor="val_loss",
            verbose=1,
            save_best_only=True,
            save_weights_only=False,
            mode="auto",
            save_freq="epoch",
        ),
        callbacks.LearningRateScheduler(
            schedule=lr_scheduler,
            verbose=0,
        ),
    ],
)

Deep Learning の勉強でおすすめの本

「イラストで学ぶディープラーニング」

「ゼロから作る Deep Learning ①」

スポンサーリンク

コメント

タイトルとURLをコピーしました