【自前AI講座】線形回帰の理論／数式／コード実装

自前AI講座用の資料です．
初回なので，まずは機械学習の中で一番単純と思われる線形回帰について，考え方や数式，Python のライブラリを用いたコード実装までを紹介します．
線形回帰とは，説明変数と目的変数の関係を線形なモデルとして表現する回帰の一種で，説明変数が１つならば単線形回帰（単回帰），複数ならば重線形回帰（重回帰）と呼びます．
「なんだ最小二乗法かよ」と残念に思われるかもしれませんが，簡易的なトレンドを見る場合においてはぼちぼちな精度で，計算も簡単で早い，かつ，解釈性が非常に高い手法であり，学んでおいて損はないと考えます．

今回のコードは github にも保存しています．

PythonCourse/013_LinearRegression at main · KazutoMakino/PythonCourse

Python Course. Contribute to KazutoMakino/PythonCourse development by creating an account on GitHub.

機械学習手法の選定について
理論と数式
コード実装と可視化例
演習問題
演習問題の回答
機械学習の勉強でおすすめの本

機械学習手法の選定について

機械学習初回なので，本題に入る前に，まずは機械学習手法はどうやって選定すれば良いかということについて紹介いたします．
と言っても，最初のステップとしては，以下の機械学習の Python ライブラリである scikit-learn のチートシートを参照するだけです．

scikit-learn: machine learning in Python

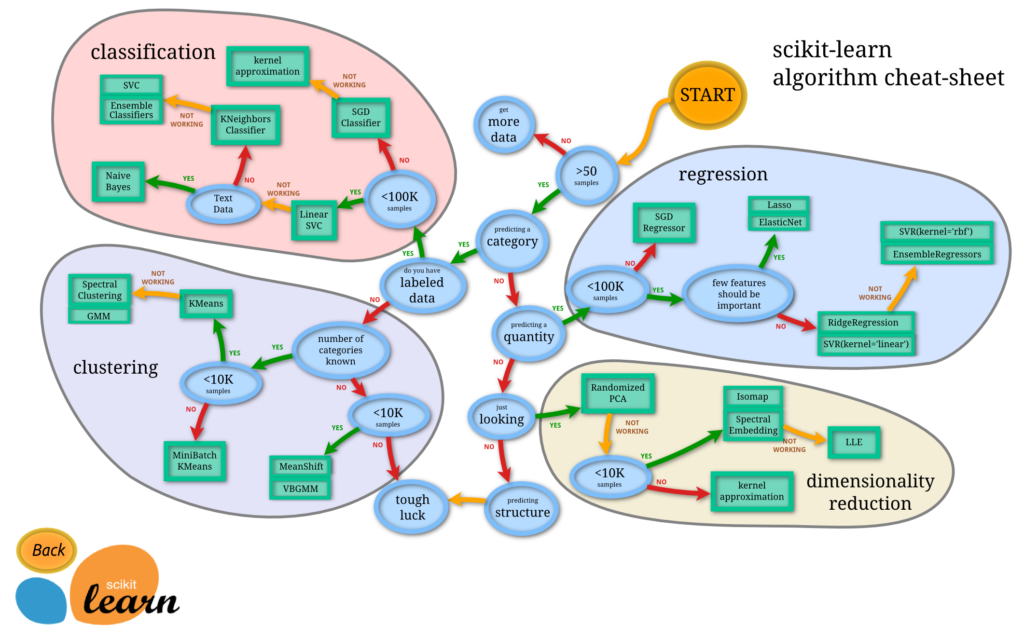
sklearn-cheat-sheet — https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html

もちろん，もっと精度を高めたいとか，カスタマイズしたいということであれば，違うライブラリを使ったり，深層学習をやってみたり，フルスクラッチ開発することになります．

理論と数式

冒頭に記載した通り，線形回帰には単線形回帰と重線形回帰があります．
まずは，簡単な単線形回帰から，理論と数式について見ていきます．

単線形回帰

単線形回帰では，説明変数が１種類のみです．
このとき，線形モデルの方程式は，次の一元一次方程式にて書き表せます．
（一元：説明変数の種類の数が１つ，一次：説明変数の最大乗数が１乗）

$$ y = ax + b $$

ここで，$a$ は説明変数 $x$ の係数，重み $b$ は $y$ 軸の切片を表します．
中学校で習いましたね．
データに最も適合する直線を回帰直線と言い，回帰直線からサンプル点への $y$ 方向のズレをオフセットまたは残差 (residual) と呼び，モデルによる推論値と真の解との誤差を表します．

各係数である重み $a, b$ を求めるには，最小二乗法を用います．
最小二乗法とは，元データとモデル関数の誤差の二乗和を最小化することで，元データを説明するのに最もらしい式を求める手法です．
具体的に各重みは，説明変数と目的変数のデータがそれぞれ $X = \{x_1, x_2, \cdots, x_n\}, \ Y = \{y_1, y_2, \cdots, y_n\}$ として与えられたとき，以下にて算出可能です．

$$
\begin{align}
& a = \frac{\textrm{Cov}(X, Y)}{\sigma_{X}^2} \\
& b = \bar{Y} – a \bar{X}
\end{align}
$$

それぞれ，$\bar{X}, \bar{Y}$：X, Y の平均値，$\textrm{Cov()}$：共分散，$\sigma$：標準偏差を表します．

線形モデル式を $y = ax + b$ とすると，離散データ $(x_i, y_i)$ の $y$ 方向の残差は $\delta_i = y_i \ – ax_i \ – b$ と書くことができます．
この残差 $\delta_i$ の二乗和が最小となるのが回帰直線となる，というのが最小二乗法であり，二乗和 $\Sigma{\delta_i^2} = \Sigma{\left( y_i \ – \ ax_i \ – \ b \right)^2} $ の最小値を考える（= 0 として解く）ことで，$a, b$ を求める式を導出できます．

$$
\begin{align}
& a で偏微分： a \Sigma{x_i^2} \ – \ \Sigma{x_i y_i} + b \Sigma{x_i} = 0 \\
& b で偏微分： nb \ – \ \Sigma{y_i} + a \Sigma{x_i} = 0
\end{align}
$$

ここで，$i = 1, 2, \cdots, n$ としています．
上記の連立方程式を解くことで $a, b$ が求まります．

重線形回帰

単線形回帰と同様，重線形回帰でもあまりやることは変わりません．
重線形回帰では，説明変数が複数ある場合の線形回帰です．
以下説明では簡単のため，説明変数は２つとします．
このとき，線形モデルの方程式は，次の二元一次方程式にて書き表せます．

$$
z = ax + by + c
$$

説明変数と目的変数のセット：$(x_1, y_1, z_1), (x_2, y_2, z_2), \cdots, (x_n, y_n, z_n)$ と上記線形モデルの残差の二乗和は $\Sigma{\delta_i^2} = \Sigma{\left( z_i \ – \ ax_i \ – \ by_i \ – \ c \right)^2} $ で，これを最小化することで $a, b, c$ が導出できます．

具体的に各重みは，説明変数と目的変数のデータがそれぞれ $X = \{x_1, x_2, \cdots, x_n\}, \ Y = \{y_1, y_2, \cdots, y_n\}, \ Z = \{z_1, z_2, \cdots, z_n\}$ として与えられたとき，以下にて算出可能です．

$$
\begin{align}
& a = \bar{Z} – b \bar{X} – c \bar{Y} \\
& b = \frac{S_{zx} S_{yy} \ – \ S_{yz} S_{xy}}{S_{xx} S_{yy} \ – \ {S_{xy}}^2} \\
& c = \frac{S_{yz} S_{xx} \ – \ S_{zx} S_{xy}}{S_{xx} S_{yy} \ – \ {S_{xy}}^2} \\
\end{align}
$$

ここで $S_*$ は以下とします．

$$
\begin{align}
& S_{xx} = \Sigma{x_i^2} \ – \ n {\bar{X}}^2 \\
& S_{yy} = \Sigma{y_i^2} \ – \ n {\bar{Y}}^2 \\
& S_{zz} = \Sigma{z_i^2} \ – \ n {\bar{Z}}^2 \\
& S_{xy} = \Sigma{x_i y_i} \ – \ n \bar{X} \bar{Y} \\
& S_{yz} = \Sigma{y_i z_i} \ – \ n \bar{Y} \bar{Z} \\
& S_{zx} = \Sigma{x_i z_i} \ – \ n \bar{X} \bar{Z} \\
\end{align}
$$

線形モデル式を $z = ax + by + c$ とすると，離散データ $(x_i, y_i, z_i)$ の $z$ 方向の残差は $\delta_i = z_i \ – \ a x_i \ – \ b y_i \ – \ c$ と書くことができます．
この残差 $\delta_i$ の二乗和 $\Sigma{\delta_i^2} = \Sigma{\left( z_i \ – \ a x_i \ – \ b y_i \ – \ c\right)^2} $ の最小値を考えることで，$a, b, c$ を求める式を導出できます．
具体的には，以下の連立方程式を解くことにより，$a, b, c$ が求まります．

$$
\begin{align}
& a で偏微分： an + b \Sigma{x_i} \ – \ c \Sigma{y_i} \ – \Sigma{z_i} = 0 \\
& b で偏微分： a \Sigma{x_i} + b \Sigma{x_i^2} + c \Sigma{x_i y_i} \ – \ \Sigma{x_i z_i} = 0\\
& c で偏微分： a \Sigma{y_i} + b \Sigma{x_i y_i} + c \Sigma{y_i^2} \ – \ \Sigma{y_i z_i} = 0
\end{align}
$$

コード実装と可視化例

工学部出身であれば，最小二乗法は大学のプログラミングの授業で for 文などを用いてコードを書いたことがあるかもしれません．
実際，前の章の関係式を愚直にコードに落とし込むことで計算が可能です．
しかしながら，Python であれば，冒頭でご紹介した機械学習用ライブラリの scikit-learn が便利ですので，こちらを用いていきます．

単線形回帰

はじめに，簡単なデータを作って，それに対して線形回帰式を計算してみましょう．
まずは，データについて準備します．

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

# 離散点 x, y を定義
x = np.arange(0, 5)
y = np.array([5, 2, 4, 3, 1])

matplotlib にて可視化してみましょう．
（matplotlib の使い方はこちら：https://slash-z.com/matplotlib-first-step/）

fig = plt.figure()
ax = plt.axes()
ax.scatter(x, y)
ax.set_xlim(-1, 6)
ax.set_ylim(-1, 6)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_aspect(aspect="equal")
fig.tight_layout()
plt.show()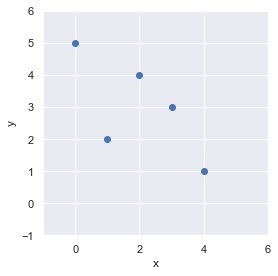

線形回帰式は，右肩下がりになりそうですね．
では，傾きを計算してみましょう．
scikit-learn を用いる前に，前の章の定義式から計算してみます．

# 傾き
a = np.cov(x, y, ddof=0) / np.std(x, ddof=0)**2
a = a[0,1]

# 切片
b = np.mean(y) - a * np.mean(x)

print(f"傾き： a = {a}, 切片： b = {b}")
# 傾き： a = -0.7, 切片： b = 4.4

傾きと切片が求まりました．
可視化してみましょう．

fig = plt.figure(facecolor="white")
ax = plt.axes()
ax.scatter(x, y, color="black", marker="x")
ax.plot(x, a*x + b, color="red")
ax.set_xlim(-1, 6)
ax.set_ylim(-1, 6)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_aspect(aspect="equal")
fig.tight_layout()
plt.show()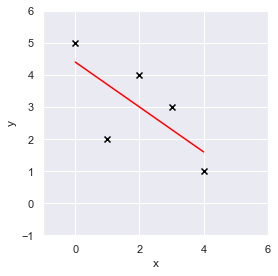

黒いバツ印がデータ点，赤の線分が線形回帰式です．
離散点を線形でモデル化できているように見えます．

上記計算について，今度は，python の機械学習ライブラリである scikit-learn を用いて算出しますが，一旦，scikit-learn の API について説明します．
scikit-learn の使い方は非常に簡単で，主に，

モデル定義（この時，パラメータも同時に定義．仮に model としてインスタンス化．）
model.fit(説明変数，目的変数) で学習
model.predict(説明変数) で，上記学習したモデルで推論を返す

これだけです．
関数によって model のメソッドは変わってきます．

注意点として，説明変数は２次元配列であることが想定されていますので，上記で設定したデータ x について配列の形を以下のように修正する必要があります．

arr = x.reshape(-1, 1)
print(f"x.shape = {x.shape}, arr.shape = {arr.shape}")
# x.shape = (5,), arr.shape = (5, 1)

説明変数を２次元配列に直したものを arr として定義し，これを用います．
今回は，LinearRegression を用いますので，まずはインポートします．

from sklearn.linear_model import LinearRegression

LinearRegression のパラメータは次です．

sklearn.linear_model.LinearRegression(*, fit_intercept=True, copy_X=True, n_jobs=None, positive=False)
- fit_intercept=True：　切片を計算する場合は True，切片を 0 として計算する場合は False にします
他の引数については気にしなくて OK です．

最初にモデルを定義します．

model = LinearRegression()

次に学習します．

model.fit(arr, y)

推論は，モデルに説明変数を渡すだけです．

pred = model.predict(arr)
print(pred)
# [4.4 3.7 3.  2.3 1.6]

簡単ですね．
LinearRegression においては，メソッドで傾きと切片が出せます．

print(f"傾き： a = {model.coef_}, 切片： b = {model.intercept_}")
# 傾き： a = [-0.7], 切片： b = 4.4

先ほど numpy を使って計算した結果と一致しました．

上記は，データ点全てを学習に用い，推論も同じデータについて算出していました．
しかしながら，現実的には，今保有しているデータで学習させ，未知のデータに対して推論したいというのが大半だと思います．
ということで，次は，データ点が多い場合も見てましょう．
まずは，以下で 0 から 100 まで 0.1 刻み幅の数列の $x$ に対し $y = x$ に $\pm 5$ をランダムに与えたデータとして定義します（numpy の使い方：https://slash-z.com/python-numpy-firststep/）．
線形回帰式は，傾きが１，切片が０になるイメージです．

# 指定乱数シードによるランダムジェネレータを設定
rng = np.random.RandomState(seed=0)

# x, y を定義
x = np.arange(start=0, stop=100 + 0.1, step=0.1)
y = x + rng.uniform(low=-5, high=5, size=len(x))
x = x.reshape(-1, 1)

print(x.shape, y.shape)
# (1010, 1) (1010,)

学習用データとモデルの検証用データを分けるため，scikit-learn の train_test_split を用います．
種々のデータ分割の手法については，こちらの記事（https://slash-z.com/data-split-of-cross-validation/）をご参照ください．

from sklearn.model_selection import train_test_split

# 学習用と評価用のデータをシャッフルせずに 6 : 4 に分ける
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4, shuffle=False)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
# (600, 1) (401, 1) (600,) (401,)

データを可視化すると，次のようになっています．

fig = plt.figure(facecolor="white")
ax = plt.axes()
ax.scatter(x_train, y_train, marker=".", label="train")
ax.scatter(x_test, y_test, marker=".", label="test")
ax.set_aspect(aspect="equal")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.legend(loc="upper left")
fig.tight_layout()
plt.show()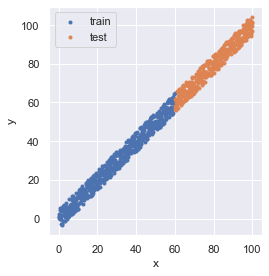

やることは変わりません．
モデル定義 → fit で学習 → predict で推論　です．

model = LinearRegression()
model.fit(X=x_train, y=y_train)
pred = model.predict(x)

ここで，推論は学習用／検証用データ全体に対して計算していますが，検証用のみ精度確認したい場合は，適宜 x の代わりに x_test としてください．
推論結果を可視化しましょう．

fig = plt.figure(facecolor="white")
ax = plt.axes()
ax.scatter(x_train, y_train, marker=".", label="train")
ax.scatter(x_test, y_test, marker=".", label="test")
ax.plot(x, pred, color="lime")
ax.set_aspect(aspect="equal")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.legend(loc="upper left")
fig.tight_layout()
plt.show()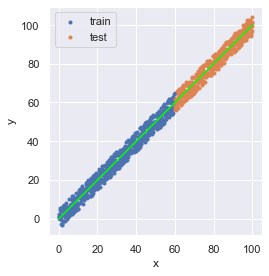

print(f"傾き： a = {model.coef_}, 切片： b = {model.intercept_}")
# 傾き： a = [1.00166797], 切片： b = -0.0679279030371518

線形回帰式は，おおよそ傾き１，切片０に無事算出されました．

重線形回帰

先ほどまでは，説明変数が１種類しかない単線形回帰でしたが，LinearRegression では重線形回帰も可能です．
同様に，デタラメに２種類の説明変数と目的変数を持つデータを作成します．

# 指定乱数シードによるランダムジェネレータを設定
rng = np.random.RandomState(seed=0)

# x, y を定義
x = rng.uniform(low=0, high=100, size=len(x))
y = rng.uniform(low=0, high=100, size=len(x))
z = x**2 + x

print(x.shape, y.shape, z.shape)
# (1001,) (1001,) (1001,)

次に学習用データと検証用のデータで 6 : 4 に分割します．

# 学習用と評価用のデータをシャッフルせずに 6 : 4 に分ける
x_train, x_test, y_train, y_test, z_train, z_test = train_test_split(
    x, y, z, test_size=0.4, shuffle=False,
)
print(
    x_train.shape,
    x_test.shape,
    y_train.shape,
    y_test.shape,
    z_train.shape,
    z_test.shape,
)
# (600,) (401,) (600,) (401,) (600,) (401,)

3D で可視化すると以下のようなプロットになります．

fig = plt.figure(facecolor="white")
ax = plt.axes(projection="3d")
ax.scatter(x_train, y_train, z_train, marker=".", label="train")
ax.scatter(x_test, y_test, z_test, marker=".", label="test")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
ax.legend(loc="upper left")
fig.tight_layout()
plt.show()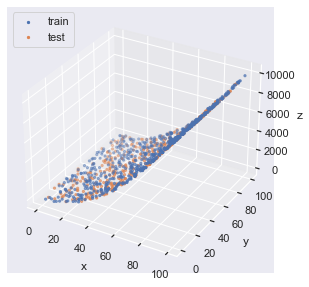

3D プロットは見にくいので，x-y, y-z, z-x 平面への射影を可視化してみます．

fig = plt.figure(facecolor="white", figsize=(10,5))

# x-y 平面に射影
ax1 = fig.add_subplot(1,3,1)
ax1.scatter(x_train, y_train, marker=".", label="train")
ax1.scatter(x_test, y_test, marker=".", label="test")
ax1.set_aspect(aspect="equal")
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.legend(loc="upper left")
ax1.set_title("x-y plane")

# y-z 平面に射影
ax2 = fig.add_subplot(1,3,2)
ax2.scatter(y_train, z_train, marker=".", label="train")
ax2.scatter(y_test, z_test, marker=".", label="test")
# ax2.set_aspect(aspect="equal")
ax2.set_xlabel("y")
ax2.set_ylabel("z")
ax2.legend(loc="upper left")
ax2.set_title("y-z plane")

# z-x 平面に射影
ax3 = fig.add_subplot(1,3,3)
ax3.scatter(z_train, x_train, marker=".", label="train")
ax3.scatter(z_test, x_test, marker=".", label="test")
# ax3.set_aspect(aspect="equal")
ax3.set_xlabel("z")
ax3.set_ylabel("x")
ax3.legend(loc="upper left")
ax3.set_title("z-x plane")

fig.tight_layout()
plt.show()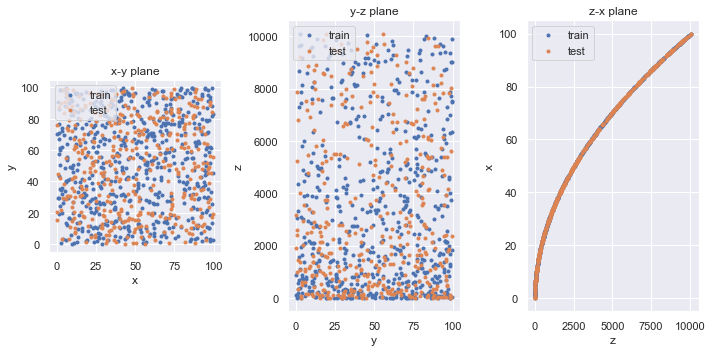

説明変数を (x_train, y_train)，目的変数を z_train として学習させるために，arr として (x, y) の２次元配列の説明変数を生成します．

arr = np.stack((x, y), axis=1)
arr_train = np.stack((x_train, y_train), axis=1)
arr_test = np.stack((x_test, y_test), axis=1)
print(arr.shape)
# (1001, 2)

重線形回帰になってもやることは同じです．

model = LinearRegression()
model.fit(arr_train, z_train)
pred = model.predict(arr)
print(pred.shape)
# (1001,)

元データと推論結果を重ねて可視化してみましょう．

fig = plt.figure(facecolor="white", figsize=(10,5))

# 3D
ax1 = fig.add_subplot(1,3,1, projection="3d")
ax1.scatter(x_train, y_train, z_train, marker=".", label="train")
ax1.scatter(x_test, y_test, z_test, marker=".", label="test")
ax1.scatter(x, y, pred, marker=".", label="pred")
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.set_zlabel("z")
ax1.legend(loc="upper left")

# y-z 平面に射影
ax2 = fig.add_subplot(1,3,2)
ax2.scatter(y_train, z_train, marker=".", label="train")
ax2.scatter(y_test, z_test, marker=".", label="test")
ax2.scatter(y, pred, marker=".", label="pred")
# ax2.set_aspect(aspect="equal")
ax2.set_xlabel("y")
ax2.set_ylabel("z")
ax2.legend(loc="upper left")
ax2.set_title("y-z plane")

# z-x 平面に射影
ax3 = fig.add_subplot(1,3,3)
ax3.scatter(z_train, x_train, marker=".", label="train")
ax3.scatter(z_test, x_test, marker=".", label="test")
ax3.scatter(pred, x, marker=".", label="pred")
# ax3.set_aspect(aspect="equal")
ax3.set_xlabel("z")
ax3.set_ylabel("x")
ax3.legend(loc="upper left")
ax3.set_title("z-x plane")

fig.tight_layout()
plt.show()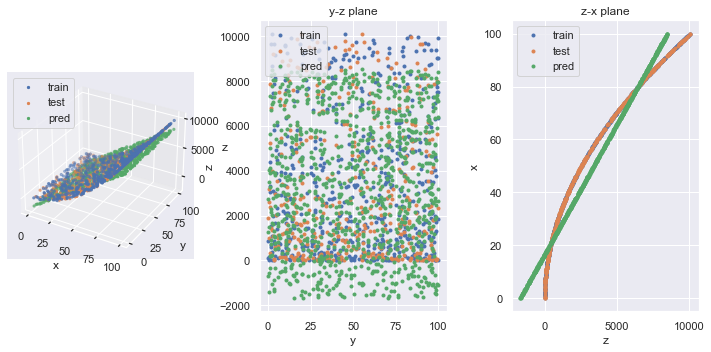

局面に対して重線形回帰しているので，3D や z-x 平面プロットに見られるように，平面で近似されています．

演習問題

Q1. ワインデータセットについて，以下を参照して，目的変数であるワインの等級を重線形回帰によって求めてください．

データ分割は train_test_split にて行い，学習用データは全データの 90 %，データのシャッフルは True としてください（結果に再現性を持たせたい場合は，引数 random_state に任意の数をせっていください）
データは，以下のコードにて読み込むことができます（データの説明はこちら：https://slash-z.com/matplotlib-first-step/）

from sklearn.datasets import load_wine

df_x, df_y = load_wine(return_X_y=True, as_frame=True)

Q2. 上記で学習したモデルを用いて，df_x 全データについて推論を計算し，分類精度を計算しましょう．
分類問題に無理やり回帰を用いていることから，推論結果は float となるため，例えば推論結果に .astype(np.uint8) としてカテゴリ変数に変換してください．
for / if 文を用いても精度は計算できますが，scikit-learn を用いて分類問題における認識精度を確認するには，以下のようにして算出が可能です．
ここで，y_true は正解ラベルの df_y，y_pred には df_x に対するモデルの推論結果を代入してください．

from sklearn.metrics import accuracy_score

print(accuracy_score(y_true, y_pred))

Q3. カリフォルニア住宅価格データセットについて，重線形回帰を用いて以下の手順で住宅価格を予測してみましょう．

次のコードでデータ読み込み，学習用／検証用にデータを分割します．

from sklearn.datasets import fetch_california_housing

df_x, df_y = fetch_california_housing(return_X_y=True, as_frame=True)
x_train, x_test, y_train, y_test = train_test_split(
    df_x, df_y, test_size=0.25, shuffle=True, random_state=0,
)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
# (15480, 8) (5160, 8) (15480,) (5160,)

学習用データ (x_train, y_train) のみを学習し，検証用データ x_test について住宅価格を予測しましょう．
上記で予測した住宅価格について，正解の値との絶対平均誤差を算出してみましょう．
以下のコードにて絶対平均誤差が算出できます．
ここで，y_true は正解データの y_test，y_pred には x_test に対するモデルの推論結果を代入してください．

from sklearn.metrics import mean_absolute_error

print(mean_absolute_error(y_true, y_pred))

演習問題の回答

演習の解答はこちら

Q1. ワインデータセットについて，目的変数であるワインの等級を重線形回帰によって求めてください．

from sklearn.datasets import load_wine
from sklearn.metrics import accuracy_score

# データ読み込み
df_x, df_y = load_wine(return_X_y=True, as_frame=True)

# データ分割
x_train, x_test, y_train, y_test = train_test_split(
    df_x, df_y, test_size=0.1, shuffle=True, random_state=0,
)

# 学習／推論
model = LinearRegression()
model.fit(x_train, y_train)
pred = model.predict(df_x)

Q2. 上記で学習したモデルを用いて，df_x 全データについて推論を計算し，分類精度を計算しましょう．

# float -> int
pred_cate = pred.astype(np.uint8)

# 分類精度算出
print(accuracy_score(y_true=df_y, y_pred=pred_cate))

Q3. カリフォルニア住宅価格データセットについて，重線形回帰を用いて以下の手順で住宅価格を予測してみましょう．

from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_absolute_error

# データ読み込み／分割
df_x, df_y = fetch_california_housing(return_X_y=True, as_frame=True)
x_train, x_test, y_train, y_test = train_test_split(
    df_x, df_y, test_size=0.25, shuffle=True, random_state=0,
)

# 学習／推論
model = LinearRegression()
model.fit(x_train, y_train)
pred = model.predict(x_test)

print(mean_absolute_error(y_true=y_test, y_pred=pred))

機械学習の勉強でおすすめの本

“Python機械学習プログラミング達人データサイエンティストによる理論と実践” は 500 ページ超もあり，理論や実装についてしっかり書かれているため，体系的・網羅的に学習できます．
しかしながら超大作であるため，初学者が全部を一から読み進めて行くという使い方だと，よほどの根気がなければ挫折すると思います．
また，数式もちゃんと書かれているのですが，基礎的な解析学や線形代数学などの知識があること前提に書かれていますので，大学のときの教科書や参考書，web 記事なども参考にする必要があります．
従いまして，見たいところだけを随時見たり，ある程度身についてきてからハンドブック的に用いることを推奨します．
筆者は，こちらの第２版を購入しており，今もハンドブック的な役割で使っています．

リンク

数学の知識について，個人的には，演習問題もついててお得な，以下の書籍をハンドブック的に参考にすることが多いです．
深く内容を見返したい場合は，大学のときの教科書や参考書を見ています．

リンク